流体流れとは

流体流れとは、力が加えられたとき、または圧力差が生じたときに、液体または気体が示す連続的な変形や運動です。一定の形状を維持する固体とは異なり、流体流れは、流体そのものの形状変化や、流体が収容されている容器に適応する能力を反映します。

流れている流体の振る舞いは、流れに対する流体の内部抵抗を示す粘度による影響を受けます。流体は、その粘度特性に基づいて、ニュートン流体または非ニュートン流体に分類されます。

流体流れを理解することは、航空宇宙、土木、機械、バイオメディカルエンジニアリングなど、多くの工学分野で不可欠となります。また、海洋学、気象学、生物学などの科学分野においても非常に重要です。複雑な流体流れの問題に対処するために、強力なコンピュータハードウェアと高度な数値解析法を組み合わせた数値流体力学（CFD）などの高度な技術が採用されています。

流体力学は、流れの測定値から導出された経験的法則に基づいて、流体や気体の運動を研究する分野です。流体流れの問題では、以下のような特性を調べます。

• 流体速度 - 流体がどの程度の速さでどの方向に移動しているかを表すベクトル量（単位: メートル/秒）です。
• 流体圧力 - 流体がその周囲または相互作用するサーフェスに作用する単位面積あたりの力を表すベクトル量（単位: パスカルまたはポンド/平方インチ）です。
• 流体温度 - 流体がどの程度高温／低温であるかを反映する、流体内の分子の平均運動エネルギーを表します（単位: 摂氏、ケルビン、華氏）。 
• 流体粘性 - 流体の流れや変形に対する抵抗の測定値（単位: パスカル秒）であり、隣接する流体層が相対的に移動する際の内部摩擦を定量化したものです。

流体力学には、空力（航空機の翼にかかる力の計算など、空気や気体の運動に関する研究分野）や流体力学（パイプラインを通る石油の質量流量の決定など、液体の運動に関する研究分野）など、多くのサブ分野があります。

流体流れにおけるレイノルズ数

変数の数を効果的に減らし、物理現象から有意義な相関関係を抽出するために、無次元数が使用されます。レイノルズ数はそのような無次元数の1つで、流体流れの慣性力を粘性力に関連付けるものです。

層流では、慣性力に比べて粘性力が大きくなります。レイノルズ数が増加すると、慣性力がより支配的になり、流れは最終的には乱流になります。これが起こるレイノルズ数は、「臨界レイノルズ数」と呼ばれています。

臨界レイノルズ数は、固定値ではなく、境界面の滑らかさや流れのジオメトリなどの要因によって変化します。たとえば、滑らかなサーフェスで囲まれた内部流れの場合、レイノルズ数の値はおよそ2,300ですが、外部流れの場合はそれよりもはるかに高くなることがあります。

流体流れは、流体に固有の特性や、空間と時間における変化を反映した、さまざまな属性を持ちます。そして、乱流の場合はさらに難しい問題があります。現在のところ、これらの問題に対する明解な解決法は導き出されていません。

層流とは、流れの中で異なる流体層（薄膜）間に混合がない流れです。層流は、粘性力が慣性力よりも強い場合に発生します。しかし、工学的に関心のある自然発生流れのほとんどは乱流に遷移します。

乱流では、流体層が混合し、発生した応力によって回転要素（循環および渦）が形成されます。乱流は、粘性力よりも慣性力が強い場合に発生します。

さらに、完全な乱流でも層流でもない、3つ目のタイプの流れとして遷移流も存在します。

エンジニアは、レイノルズ分解を用いて乱流を研究しています。このレイノルズ分解では、流れが平均成分と摂動成分に分けられます。レイノルズ数は、流体内の粘性力に対する慣性力の比として定義されており、特定の構成で流れが層流であるか乱流であるかを判断するのに役立つ無次元量です。これは次式によって得られます。

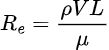
ここで、ρは流体密度、Vは流れの速度、Lは特性長さ（パイプの直径など）です。

たとえば、以下の特性を持つパイプを考えてみましょう。

• R_eが2,000未満の場合、粘性力が支配的であり、流動様式は層流となります。
• R_eが4,000を超える場合、慣性力が支配的であり、流動様式は乱流となります。
• R_eが2,000～4,000の範囲の場合は、遷移流となります。

以下に、層流と乱流の主な違いを示します。

定常流れと非定常流れ

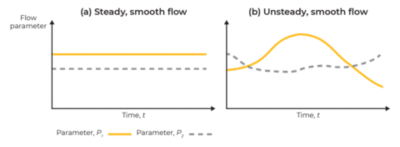
定常流れとは、速度、圧力、密度などの特性が空間内の任意の点で時間とともに変化しない流れです。反対に、これらの特性のいずれかが時間とともに変化する場合は、非定常流れとなります。

乱流は、本質的に非定常です。ただし、統計的に定常（つまり、速度などの時間平均流れ条件は時間とともに一定のまま）のこともあります。

非定常流れは自然界でよく見られます。ただし、非定常流れモデルの解析は、時間次元が導入されることで非常に多くの計算能力が必要となるため、より困難になります。

一様流れと非一様流れ

一様流れとは、流れ全体で流体の速度が方向および大きさで一定に保たれる流体の流れを表します。

圧縮性流れと非圧縮性流れ

圧縮性とは、流体内の分子をどの程度近づけられるかという能力を表します。 

気体は、分子が互いに離れているために圧縮しやすい特性があります。圧力をかけたり緩和したりすることで、気体の体積や密度を簡単に変更できます。一方、液体は分子が互いに非常に近いため、圧縮が困難です。 

実用的な用途では、液体は非圧縮性と見なすことができます（非定常流れ問題のように、サウンドの伝播が重要になる場合を除く）。

その流体内における音速に対して速度変化が小さい流れ場では、（気体の場合でも）流体流れを非圧縮性として扱うことができます。これは、圧縮性効果によって支配方程式の複雑さが大幅に高まるため、重要になります。

マッハ数は、流体流れにおける圧縮性効果の重要性を判断するのに役立つ無次元数です。マッハ数が0.3以下の場合、流れを非圧縮性として扱うことができます。より高速な流れ（高亜音速および超音速）では、特に衝撃波が関与する場合（ジェットエンジン、高速航空機、ロケットなど）に、圧縮性効果が重要になります。

粘性流れと非粘性流れ

粘度は、流体内の摩擦を測定したものです。流体内の層が互いに擦れることで摩擦が生じます。高粘度（蜂蜜など）は摩擦量が高いことを示します（逆も同様）。液体の場合、温度が上昇するにつれて粘度は低下します。これは、暖かい液体内の方が分子はより自由に移動し、互いに滑りやすくなるためです。それに対して気体の場合、温度が上昇するにつれて粘度は高まります。

単一流れと多次元流れ

流れの次元は、流れの特性に大きな影響を与える空間次元の数を指します（時間も、多くのケースで「次元」と呼ばれる）。

1次元流れでは、速度、圧力、密度などの量が1次元でのみ大きく変化します。1次元流れモデルは、他の2つの次元での変化が無視できる流れ条件である（たとえば、直径が一定のパイプで、パイプの長さに沿ってのみ変化が生じる）ときに有用です。

2次元流れモデルでは、第3次元の変動は一様であるか、または無視できるかのいずれかです。これは、ある次元が別の次元よりもはるかに大きい高アスペクト比の流れで発生します。たとえば、平板に沿った境界層の発達では、平板の長さや高さに沿った変化と比較して、平板の幅に沿った流れ特性の変化を無視できます。また、多くの気象システムモデルは、地表面と比較して地球の大気が非常に薄いため、2次元となります。

3次元流れモデルは、エンジニアリング分野で最も普遍的であり、流れの複雑さを3次元で完全に捉えることができます。これらのケースでは、複雑なジオメトリによって複雑な流体運動が発生しますが、圧力、速度、密度などの量の3次元での変動の影響も受けます。

単純化された1次元モデルや2次元モデルでは解析作業が軽減されますが、必ずしも有効なオプションではありません。選択すべきモデルは、検討対象の問題によります。多くのケースでは、設計の初期段階では単純化されたモデルを使用し、最終検証段階では高度な3Dモデリングを使用します。

外部流れと内部流れ

外部流れと内部流れの主な違いは、これらの流れを囲む境界の性質に起因します。

少なくとも一方の側が境界なしの場合に外部流れが発生し、境界層と後流効果が発生します。一方、内部流れは、囲まれた（固体の）境界内で発生し、主に圧力損失や流れの分布が調査対象となります。

外部流れの例は、航空機の胴体上を流れる空気（揚力や抗力などの空力が注目される）、船の船体を横切る水、建物の上を吹く風などです。オブジェクトの形状と向きは、外部流れ、形成される境界層（オブジェクトと流れの境界面の粘性領域）、および流れの剥離の振る舞いの影響を与えます。

内部流れの例は、パイプやダクトを流れる空気や水です。この場合、流れは境界壁に囲まれており、壁によって運動量を失うと、流れの方向に沿って圧力が低下します。

混相流

混相流とは、2つ以上の異なる熱力学的相が同時に発生する流れです。これらの相は、気体、液体、または固体であり、水蒸気、油／水の流れ、固体-液体懸濁液など、同一または異なる成分で構成されることがあります。

混相流は、通常は二相流と三相流に分類されますが、複雑な系には追加の相が含まれることもあります。

一般的な二相流には、以下のものがあります。

• 気体-液体流れ — 蒸発器や凝縮器に見られる
• 気体-固体流れ — バイオリアクターに見られる
• 液体-固体流れ — スラリー輸送および堆積システムに見られる

三相流としては、気液固流（化学反応器や流動床など）や気液-液流（石油回収システムで見られる）があります。

混相流のモデリングは、異なる相間の相互作用によって複雑になります。これは化学処理および医薬品（撹拌、ろ過、剥離など）、発電（蒸気タービンおよび燃焼モデリング）、石油およびガス（フレアリングおよび通気の低減）など、さまざまなエンジニアリング問題で極めて重要となります。こうした問題の解決には、オイラー-ラグランジュ法、オイラー-オイラー法、またはVOF法などのアプローチが採用されています。

ナビエ–ストークス方程式に基づく乱流の直接数値シミュレーション（DNS: Direct Numerical Simulation）（乱流モデリングを除く）は、中程度のレイノルズ数で実行できます。しかし、非常に多くの計算リソースが必要となり、多くのエンジニアリングフローでは直接数値シミュレーションを実行するにはレイノルズ数が高すぎます。たとえば、人間を運ぶのに十分な大きさの飛行体は、DNSの到達範囲を超えています（Re = 4,000,000）。

こうした理由から、エンジニアはレイノルズ平均ナビエ-ストークス（RANS）方程式と乱流モデリングを組み合わせて、乱流の特性を適切に評価します。RANSモデルでは、レイノルズ応力を介して、乱流によって生じる追加の運動量と熱伝達が考慮されます。RANSモデルは、さまざまなタイプの乱流に対して適切な精度をもたらしながら、DNSよりも計算負荷が低いため、エンジニアリング分野で広く使用されています。

ラージエディシミュレーション（LES）とそのバリアントは、DNSとRANSの中間点を提供する別のモデリングアプローチです。LESでは、より大きな規模の乱流を直接解き、より小さな規模の乱流をモデル化することで、RANSよりも精度が高くなります。自動車の外部空力やガスタービンエンジン内の燃焼など、非定常性が重要な流れをモデル化する場合には、この手法が不可欠となります。 

流体流れを理解することは、効果的な計算モデルを開発するための最初のステップです。層流の解は比較的単純であるため、決定論的な数学モデルを使用できます。ただし、こうしたモデルの適用範囲は限られています。 

大半の実用的な問題には乱流が伴い、非定常で非決定論的な性質を持つため、モデル化が最も困難となります。乱流を正確にモデル化することは、今後もエンジニアが積極的に取り組むべき課題となるでしょう。

Ansys Fluentは、高度な物理モデリング機能と高い精度で知られる、業界をリードする流体シミュレーションツールです。

Fluentは、複雑な流体シミュレーション問題に対して効率的かつ正確なソリューションを提供する強力なツールです。以下のような、さまざまな物理モデルと手法を提供します。

• 各種の乱流モデル 
• 次数低減モデリング
• 各種の混相流モデル
• 多数の燃焼モデル
• 流体-構造連成解析
• メッシングと解析のための拡張性に優れた並列機能

関連リソース