RLC回路とは

RLC回路は、抵抗器、インダクタ、およびコンデンサが直列または並列に接続された電気回路です。RLC回路の名称は、回路図でこれらの要素を表すために使用される記号（抵抗器の「R」、インダクタの「L」、コンデンサの「C」）に由来しています。

最新の通信システムは、RLC回路とトランジスタやダイオードなどの能動素子を組み合わせて完全な集積回路を形成しています。集積回路において、RLC回路はフィルタ、増幅器、または発振器として機能し、共振や減衰などの特性に依存して動作します。たとえば、無線受信機のRLC回路は、バンドパスフィルタリングを実行し、ユーザーが特定の無線周波数を受信して他の周波数を除外できるようにします。

RLC回路は二次回路とも呼ばれます。これは、回路設計者が二階微分方程式を使用してRLC回路内の電圧と電流の特性評価を行うことに由来します。最も単純なものは直列トポロジーや並列トポロジーなどですが、回路内の各R、L、およびC要素は、さまざまなトポロジーに配置できます。

純粋なRL回路およびRC回路では、インダクタ（L）またはコンデンサ（C）の形で1つのエネルギー貯蔵要素のみが存在します。どちらの場合も、回路設計者は初期条件を1つだけ指定することで、一階微分方程式が得られます。

それに対して、RLC回路は、両方のエネルギー貯蔵要素を含むため、2つの初期条件が必要となり、二階微分方程式が得られます。これらの初期条件は、回路内に存在する初期電圧および電流に関係しています。

また、20世紀初頭までは、二階微分方程式が物理系の挙動を完全に記述すると考えられていました。しかし、Max Planckによる量子力学の原理の定式化により、現在ではこの考え方は変化しています。

一方で、二階微分方程式は現在でも多くの物理系の挙動を正確に記述しています。その一例が振り子の揺れです。振り子が放出されると重力場の位置エネルギーが運動エネルギーに変換され、最大高さに達すると、その運動エネルギーが位置エネルギーに再び変換されます。振り子から（摩擦により）エネルギーが散逸すると、徐々に静止状態に近づきます。

振り子系の例のように、二階微分方程式は周期的なエネルギー交換がある系を正確に記述します。この周期的なエネルギー交換は、電気エネルギー場と磁気エネルギー場の間に周期的な交換があるRLC回路の挙動とよく似ています。

抵抗器、インダクタ、コンデンサを組み込んだRLC回路は、電気回路設計の基礎を成します。これらの各要素は、回路の全体的な挙動に寄与する特定の物理特性を持っています。

抵抗器

抵抗器は、電流の流れに抵抗する集中回路要素であり、それによって電圧を低下させます。また、印加された信号の周波数に依存しない一定の抵抗（単位: オーム）によって特徴付けられます。抵抗器は、RLC回路内の平衡を維持するために不可欠な要素です。

インダクタ

インダクタは、通常はワイヤのコイルから構成され、電流がワイヤを通過するときに磁場にエネルギーが蓄えられます。電流の変化を抑えようとする抵抗力であり、その大きさを誘導性リアクタンス（単位: オーム）と呼びます。この誘導性リアクタンスは、印加された信号の周波数に依存します。周波数が高くなると誘導性リアクタンスが増加し、その逆も同様です。

コンデンサ

インダクタが磁場内にエネルギーを蓄えるように、コンデンサは電場内にエネルギーを蓄えます。コンデンサは、電圧の変化を抑えようとする抵抗力であり、その大きさを容量性リアクタンス（単位: オーム）と呼びます。容量性リアクタンスも周波数に依存します。周波数が高くなると容量性リアクタンスが減少し、その逆も同様です。

RLC回路は、電源と共振器の2つの主要要素で構成されています。また、テブナンとノートンの2種類の電源と、直列LCと並列LCの2種類の共振器があります。直列および並列RLC回路は、それぞれ異なる特性を持ち、それぞれが特定の用途に適しています。

直列RLC回路の特性

直列RLC回路では、抵抗器、インダクタンス、およびコンデンサが単一の回路経路上に配置され、各コンポーネントを流れる電圧が変化しても電流は変化しません。実際の影響は次のとおりです。

• 抵抗器全体で、電圧は電流と同じ位相になります。
• インダクタ全体で、電圧は電流より90度進みます。
• コンデンサ全体で、電圧は電流より90度遅れます。

その結果、回路全体での電圧は、各コンポーネントの電圧の代数和ではなく、ベクトル和になります。これらの電圧は、電流ベクトルを基準として用いてフェーザ図にプロットできます。

キルヒホッフの電圧則（KVL）は、閉回路の電圧の合計が、この回路にかかる起電力（EMF）の合計に等しいことを示しています。したがって、ソース電圧VS（単位: V）は次式で表されます。

VS = VR + VL + VC

直列RLC回路で以下を仮定すると、

VR = IR

VL = LdI/dt

VC = Q/C

次式のようになります。

VS = IR + LdI/dt + Q/C

ここで、Iは電流、Lはインダクタンス、Qは電荷、Cは静電容量です。

どのような回路でも、電流の流れに一定の抵抗が生じます。これはインピーダンス（単位: オーム）と呼ばれます。インピーダンスは、抵抗部分（直流電流に対する抵抗）とリアクタンス部分（交流電流に対する抵抗）で構成されています。直列RLC回路の場合は、次式で表されます。

Z = √R2 + (XL2 - XC2)

ここで、XLは誘導性リアクタンス（インダクタにおける交流電流に抵抗する力）、XCは容量性リアクタンス（コンデンサにおける交流電圧に抵抗する力）です。

以下に示すように、誘導性リアクタンスと容量性リアクタンスはどちらも周波数に依存します。 

• XL> XCのとき、回路全体でのリアクタンスは誘導性になり、電圧の位相は電流よりも90度進みます。 
• XL< XCのとき、回路は容量性になり、電圧の位相は電流よりも90度遅れます。  
• XL = XCのとき、回路は共振状態になります。これは、電子回路にとって重要なさまざまな用途に活用されています。

並列RLC回路の特性

並列RLC回路では、各コンポーネントを流れる電流が変化しても、R、L、およびC成分の電圧は同じままです。並列RLC回路は直列回路と相互関係にありますが、その数学的扱いはより高度です。

回路を流れる総電流は、各要素を流れる電流の代数和ではなく、ベクトル和に等しくなります。

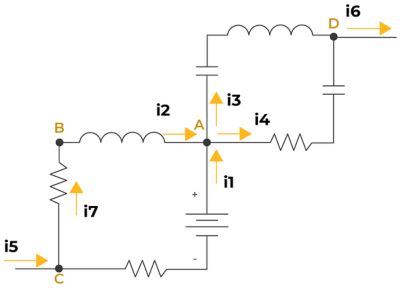
キルヒホッフの電流則（KCL）は、回路内のノードを流れる電流の合計がゼロになることを示しています。したがって、回路内の任意ノードにおけるソース電流は次式で与えられます。

IS - IR - IL - IC = 0

インピーダンスは以下となります。

1/Z = √(1/R)2 + (1/XL - 1/XC)2

上記の式は、直列RLC回路のインピーダンスの式の逆数であることがわかります。実際に、電気回路には双対関係が存在するため、並列RLCの特性は直列RLCの特性を反映しています。したがって、並列RLCのインピーダンスは直列RLCの双対であり、式は同じ一般形式を採用しています。

インピーダンス（1/Z）の逆数は、アドミタンス（単位: ジーメンス）と呼ばれます。並列回路、特に複数の分岐を伴う場合に、インピーダンスを計算するための便利な方法となります。並列回路の全アドミタンスは、単純に各要素のアドミタンスの和となります。それに対して、直列回路では、全インピーダンスは各要素のインピーダンスの和です。

なお、抵抗の逆数（1/R）はコンダクタンスとして知られ、リアクタンスの逆数（1/X）はサセプタンスとして知られています。

直列RLC回路と並列RLC回路における違い

前述したように、直列回路と並列回路の式は、互いの逆数となります。回路設計者は、これに基づいて、直列構成と並列構成のどちらが対象設計に適しているかを判断します。以下の表に、直列RLC回路と並列RLC回路の主な相違点を示します。

基本的に、RLC回路の挙動を記述するパラメータは2つ（共振周波数と減衰係数）あります。エンジニアは、これらの最初の2つから帯域幅やQ値など、他のパラメータを導出できます。

RLC回路の共振

RLC回路の重要な特性の1つが、共振周波数と呼ばれる特定の周波数で共振することです。物理系には、直ちに振動する固有振動数があります。共振状態では（駆動源の有無にかかわらず）、振動が大幅に増幅され、効率的なエネルギー伝達が行われます。

RLC回路では、コンデンサの電場に蓄えられたエネルギーがインダクタの周囲の磁場に伝達され、蓄積されます（逆も同様）。この伝達は周期的に発生し、RLC回路が発振します。共振状態において、角度周波数ω（単位: ラジアン）は次式で与えられます。

ω = 1/√LC

また、共振状態では、誘導性リアクタンスは容量性リアクタンスに等しく、回路の全インピーダンス（複素数）はゼロです。

そのため、インピーダンスは直列RLC回路では最小になり、並列回路では最大に達します。 

RLC回路における共振を理解し、適用することは、特に通信、電力システム、信号処理において、効率的で効果的な電子システムを設計するために不可欠です。重要な共振アプリケーションには、以下のものがあります。

• 周波数選択: RLC回路は、共振状態で特定の周波数の信号に応答し、他の周波数を除外できます（ラジオのチューナーなど）。
• フィルタリング: RLC回路は、バンドパス、バンドストップ、ローパスフィルタ、ハイパスフィルタなど、さまざまなタイプのフィルタとして機能します。あるいは、これらの回路を集積回路のノイズフィルタとして使用することもできます。また、特定の周波数で電流を抑制するリジェクタ回路としても機能します。このタイプの並列回路は、反共振器と呼ばれます。
• 電圧倍増: 抵抗が最小であるとき、インダクタおよびコンデンサ全体での電圧は、入力電圧の数倍となることがあります。この電圧倍増効果は、回路のQ値に比例します。
• インピーダンス整合: 共振状態では、直列RLC回路のインピーダンスは純抵抗であり、最小値となるのに対して、並列RLC回路のインピーダンスは最大値となります。これをインピーダンス整合に活用できます。
• 電力伝送: 直列RLC回路は、共振状態で電力伝送能力が最大になるため、効率的なエネルギー伝達を必要とするアプリケーションにとって重要です。
• 発振回路: RLC回路は、特定の周波数で持続的な発振が必要となる発振器に応用されています。このような場合、回路の抵抗を最小化（直列回路の場合）または最大化（並列回路の場合）することで、減衰を低減させ、理想的なLC回路を近似します。

RLC回路の減衰

減衰は、発振するRLCシステムで、振動振幅が時間とともに（抵抗によって）減少する傾向を表します。したがって、抵抗器はRLC回路内のエネルギーを散逸させる上で重要な役割を担います。また、回路が自然に（駆動源がない場合に）共振するかどうかも決まります。

RLC回路では、以下の3つのタイプの減衰応答を確認できます。

• 振動の減衰が遅いことが特徴となる不足減衰回路
• 振動がすぐに止まる過減衰回路
• 定常状態の振動に到達するのに必要な臨界時間よりもわずかに短い時間で振動が停止する臨界減衰回路
• 臨界減衰回路の場合、\zeta = 1

無次元減衰比は、RLC回路の減衰特性を評価する上で役立つ重要なパラメータです。発振回路を設計する場合、直列回路の抵抗を最小限に抑えながら、並列回路の抵抗を最大化することで、減衰を最小限に抑えます。バンドパスフィルタでは、目的の帯域幅に一致するように減衰係数が調整されます。値が大きいほど帯域幅が広くなります（逆も同様）。

RLC回路で導出されるパラメータには、帯域幅とQ値があります。

帯域幅

帯域幅は、RLC回路が共振する周波数の範囲を表します。これは、フィルタ設計における重要なパラメータであり、共振状態近くのインピーダンスの急速な変化を利用して、共振周波数に近い信号を通過（バンドパスフィルタの効果）または遮断（バンドストップフィルタの効果）することができます。

帯域幅は、カットオフ周波数間の周波数ギャップを表し、通常は回路を通過する電力が、共振状態において通過する電力の半分である周波数として定義されます。 

エンジニアは、目的の帯域幅に合わせてフィルタ回路内の減衰を調整します。減衰を高くすると、広帯域フィルタが得られます。反対に、減衰を低くすると、狭帯域フィルタになります。

Q値

無次元のQ値は、振動系が減衰する量を表します。これは、振動周期の1ラジアンで失われたエネルギーに対する、系に蓄積された初期エネルギーの比として定義されます。

Q値が高いほど、振動がよりゆっくりと消滅し、エネルギー損失率が低くなり（狭帯域、不足減衰）、Q値が低いほど損失のあるネットワーク（広帯域、過減衰）となります。Q値が高いシステムの例としては、クロック、レーザー、音叉などがあります。音叉のQ値は1000程度、一部のレーザーは1011以上の高いQ値を示します。

抵抗器、インダクタ、コンデンサを組み込んだRLC回路は、回路設計の基盤となります。エンジニアは、共振と減衰という回路特性を活用して、さまざまな分野に採用される各種の回路を設計できます。したがって、RLC回路を理解し、その特性を評価することは、さまざまなエレクトロニクスおよび通信システムで採用される回路の設計、解析、および最適化に不可欠です。

RLC回路の電磁結合は、周波数応答、電力伝送、減衰、その他の特性に影響を及ぼし、回路の性能に大きく影響する重要な要因です。

そのため、回路の設計者は、ポストLVS RLCk抽出ソフトウェアであるAnsys Exalto®を使用することで、集中定数素子寄生成分を抽出し、電気的結合、磁気的結合、および基板結合の正確なモデルを生成し、設計階層内の異なるブロック間の未知のクロストークを正確に把握できるようになります。ExaltoはほとんどのLVSパッケージに対応しており、お使いのRC抽出ツールを補完します。

さらに、プリLVS電磁界モデリングソフトウェアであるAnsys RaptorH™を使用することで、電力グリッド、フルカスタムブロック、スパイラルインダクタ、クロックツリーなど、高速RFおよびデジタルSoCの大容量電磁界モデリングが可能になります。これは、ゴールドスタンダードのAnsys HFSS™電磁界シミュレーションエンジンと、シリコンに最適化されたAnsys RaptorXエンジンを組み合わせたものです。

関連リソース