-
United States -
United Kingdom -
India -
France -
Deutschland -
Italia -
日本 -
대한민국 -
中国 -
台灣
-
-
產品系列
查看所有產品Ansys致力於為當今的學生打下成功的基礎,通過向學生提供免費的模擬工程軟體。
-
ANSYS BLOG
November 14, 2022
混合分析:建立混合數位孿生的工具
組
混合數位孿生是一種結合物理和數據的數位孿生。換句話說,混合數位孿生不僅僅只依賴模擬或者僅機器學習單獨進行(Machine Learning;ML),而是萃取這兩種方法之精華與優勢來利用系統所有可用知識。工程領域負責提供物理模型,而數據為該模型提供了新的見解補充。結合物理和數據技術
透過 Ansys Twin Builder 和混合分析工具組合,您可以將數位孿生的精準度提升至 98% 或更高。
混合分析是一組機器學習工具,以不同的方式將物理和數據組合在一起。透過在選擇培訓數據和機器學習技術方面做出更明智的選擇,您可以為混合數位孿生開啟新的可能性。其中,最明顯的一個領域是融合建模,即至少將兩種不同類型的資料組合起來訓練一個機器學習模型。
融合建模:融合物理和資料
構建一個機器學習模型時,使用者須提供輸入/輸出(Input/Output;I/O)數據,然後機器學習演算法會創建一個深度學習之模型可用於重複預測不同輸入情境下其輸出結果。自然地,深度學習所需之資料的選擇都會影響結果的品質與穩定性。例如,簡化模型(Reduced-Order Models;ROM)通常使用在模擬的資料來構建,會依賴於模擬軟體之演算法方程式之技術成熟度。實際量測資料之統計更適合為噪音感測器之學習資料。在融合建模中,至少使用兩個不同來源的資料來訓練模型。這可能意味著組合不同類型的模擬資料或組合模擬資料和感測器數據。無論如何,組合多個數據來源可以為更多的應用程式創建更豐富的機器學習模型。

融合:殘差建模
想要透過物理建模保留已知系統資訊,並從任何可用資料中學習,同時使用模擬和感測器資料是理想的。當元件或系統的基本物理被充分理解與解析後,並且用推演出之知程式進行建模時,基於這樣的物理方程式所建構之模型,可視為良好的數位元孿生模型。然而,在實踐中,由於多種原因,完整的物理模型可能很難實現,包括:
- 摩擦或損失未被完全理解。
- 幾何形狀未被充分捕獲。
- 未建模的環境影響。
- 隨著時間的降解。
例如,這可能包括電機常數的不確定性,各元件的慣性,或管道內壁摩擦的數量。在這些情況下,解決方案的第一種方法是嘗試從可用資料中去學習物理模型的參數。機器學習技術能使您從資料中去學習更準確的參數值,並為這些參數提供預測。
這種方法的一個關鍵優點是,物理行為的知識完全保留於模型中。從資料中學到的資訊會包含隱含在模型參數的值中。因此,即使模型沒有完全以物理方式呈現,並且試圖藉由調整參數來彌補,學習到的行為至少在該模型的上下文和與其他參數值的關係中是可以被解釋的。因此,設計師和工程師可以更好地瞭解問題的根本原因和系統的行為。
即便是最完善的物理模型有時也可能無法完全捕捉到系統的實際行為。具體來說,當系統中存在建模時候未考慮的物理因素時,學習更好的參數值仍然不足以達到應用所需的精度水準,因為並未把此物理行為在建模時候納入考慮。這就是融合模型可以幫助提供高度準確預測的地方。
當標定的模型和預期行為之間仍然存在差距時,您可以構建融合模型來評估孿生預測和代表目標行為資料之間的差異。這種類型的融合建模通常稱為殘差建模。在融合殘差模型中,兩個不同的資料來源是物理模型預測和實驗資料。因此,殘差建模主要用於在「假設」情景中以實現更精準的預測。

此圖展示融合殘差的建模的過程,即使用物理學模型預測和實驗資料作為兩個主要的資料來源。
這種方法的一個最大的優點是:無論你對於物理行為掌握了多少,藉由數據資料都可以幫助您模擬未知或錯誤理解的效應而留下的剩餘部分,稱之殘差數據。值得注意的是,模型的融合部分不會解釋缺失的內容,但與孿生輸出結合使用,可以提供更準確的預測。以這種方式,不確定性被限制在已知的行為部分,而透過添加機器學習使沒有任何東西會損失。
透過以這種方式應用融合模型,機器學習可以在保留已知物理的情況下進行。本質上,可以構建融合殘差模型來彌補極度糟糕的物理模型。在這些情況下,融合模型更像是資料模型,就像其他資料模型一樣,底層的物理學可能會被掩蓋或丟失。儘管如此,在這種情況下,不太好的物理模型至少可以對機器學習的部分提供一些約束。
當融合用於改善已經提供良好的保真度,但缺少約 10% 的模型時,殘差建模真正發揮作用。在這種情況下,融合模型可能無法完全解釋小的殘差的物理學,但系統的主要物理效應在物理雙胞胎中完全得到保留,並且可以輕鬆訪問。
融合建模:多信度回歸
融合建模的另一個應用是多信度回歸。在這種情況下,一種數據來源被視為基本事實,第二種數據來源則近似於該基本事實。當基本事實數據稀缺而近似數據豐富時,就會使用融合建模。其中一個例子是在測試臺上的測試。收集測試數據可能會耗費大量時間和成本,因此,人們會盡可能地將測試轉移到虛擬領域以節省成本。模擬模型可以用來替代測試臺上的測試,但前提是它們必須準確地重現系統的實際行為。從測試臺上至少需要幾個數據點來檢查模擬模型的行為。如果模擬模型不能提供與測試數據足夠高的相似度匹配,就可以建立一個融合模型來模擬測試數據和模型之間的差異。
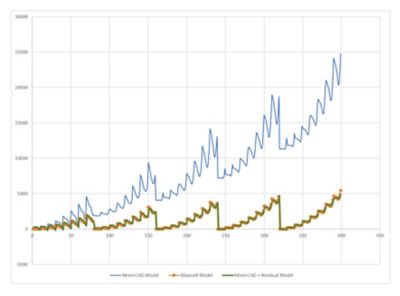
上圖展示一個 Ansys Maxwell 模型產生比 Ansys Motor-CAD 模型高得多的結果。然而,Motor-CAD 模型與融合殘差模型相結合的結果與完整的 Maxwell 模型差不多。
有了融合校正模型,就可以使用該模型來精確地模擬其他未進行測試的設計點或場景。相同的概念也可以應用在兩個模擬數據來源上。
例如,一個電動馬達的有限元素(Finite Element;FEA)模型包括完整的幾何和物理效應,可以提供非常準確的預測。但是,FEA 模型的運行時間可能很長,這可能使得在許多場景下進行重複測試變得困難。電動馬達也可以使用 1D 或 2D 假設更快地進行良好的近似建模。
融合模型使用兩種模擬的電動馬達模擬,以更快地實現最佳預測。FEA 模擬數據被用作對少數設計點的行為進行校準。1D 模型模擬所有設計點。融合模型展示了兩個模擬模型在設計點上的差異。1D 模型再加上融合校正就是其他設計點的準確預測。
FEA 模型中所需的設計點數量取決於兩個模型的結果之間的相關性。例如,如果相關性更高,可以使用 FEA 設計點,並更多地依賴於 1D 模型。
探索混合分析技術的第一手資訊
數字孿生通常存在於邊緣或雲端環境中,當中的知識可能很稀缺。混合數字孿生透過利用所有可用數據並提供最佳的預測性維護和性能優化解決方案來克服這一挑戰。儘管分析通常指從數據中學習,但混合分析是一組從實驗數據和基於物理模擬的模擬數據中學習的技術。由多種數據源和物理模型構建的融合模型是混合數字孿生體的重要組成部分,特別是在物理方面不確定的領域中,可以實現更高的準確性。










