什么是RLC电路？

RLC电路是指由电阻器、电感器和电容器以串联或并联方式连接的电路。其名称源于电路图中用于表示这些元件的符号，即“R”表示电阻器，“L”表示电感器，“C”表示电容器。

现代通信系统将RLC电路与晶体管和二极管等有源元件相结合，形成完整的集成电路。在集成电路中，RLC电路可用作滤波器、放大器或振荡器，依靠谐振和阻尼等特性来工作。例如，在无线电接收器中，RLC电路执行带通滤波，使用户能够调谐到特定的无线电频率，而排除其他频率。

RLC电路也被称为二阶电路，因为电路设计人员使用二阶微分方程来表征这些电路中的电压和电流。此外，这些电路中的每个R、L和C元件都可以排列成许多不同的拓扑，其中最简单的是串联拓扑和并联拓扑。

在纯RL和RC电路中，只有一个储能元件以电感器（L）或电容器（C）的形式存在。在这两种情况下，电路设计人员只需指定一个初始条件，就会得到一阶微分方程。

相比之下，RLC电路包含两个储能元件，因此需要两个初始条件，并得到二阶微分方程。这些初始条件与电路中存在的初始电压和电流有关。

值得注意的是，直到20世纪初，人们还认为二阶微分方程可以完整描述物理系统的行为。然而，随着Max Planck在制定量子力学原理方面所做的努力，这种观点现在已经改变。

尽管如此，二阶微分方程仍能准确描述许多物理系统的行为。一个典型示例就是钟摆的摆动，当钟摆释放时，重力场中的势能转化为动能，然后当钟摆达到最大高度时，动能又转化为势能。随着钟摆的能量耗散（由于摩擦），它逐渐静止。

碰巧的是，二阶微分方程可准确描述存在周期性能量交换的系统，如钟摆系统所示。这种周期性能量交换反映了RLC电路的行为，其中电场和磁场之间存在周期性能量交换。

RLC电路由电阻器、电感器和电容器组成，是电路设计的基础。每个元件都具有特定的物理特性，对整体电路行为有重要影响。

电阻器

电阻器是集总电路元件，可“阻挡”电流流动，从而导致电压下降。其特点是恒定电阻（以欧姆为单位），该电阻与施加信号的频率无关。电阻器在维持RLC电路的平衡方面起着不可或缺的作用。

电感器

电感器通常由线圈构成，当电流通过导线时，将能量储存在磁场中。它们会阻碍电流的变化，阻碍的程度称为感抗（以欧姆为单位）。感抗取决于施加信号的频率，随着频率的增加而增加，反之亦然。

电容器

电感器在磁场中储存能量，而电容器则在电场中储存能量。电容器会阻碍电压变化，阻碍的程度称为容抗（也以欧姆为单位）。容抗也与频率有关：其随着频率增加而减小，反之亦然。

RLC电路主要由两个部分组成，即电源和谐振器。此外，还有两种类型的电源：Thévenin和Norton电源，以及两种类型的谐振器：串联LC和并联LC谐振器。串联和并联RLC电路各自具有不同的特性，使其适用于特定应用。

串联RLC电路的特性

在串联RLC电路中，电阻器、电感器和电容器排列在单个电路路径上，这样流经每个元件的电流保持不变，而电压则各不相同。其最终效果是：

• 在电阻器中，电压与电流同相。
• 在电感器中，电压领先电流90°。
• 在电容器中，电压滞后电流90°。

因此，电路上的总电压不是每个元件上电压的代数和，而是其矢量和。以电流矢量为参考，可以将这些电压绘制在相量图上。

基尔霍夫电压定律（KVL）指出，闭合电路中的电压之和等于该电路上的电动势（EMF）之和。因此，源电压VS（以伏特为单位）为：

VS = VR + VL + VC

在串联RLC电路中：

VR = IR

VL = LdI/dt

VC = Q/C

这就变成了：

VS = IR + LdI/dt + Q/C

其中I是电流，L是电感，Q是电荷，C是电容。

任何电路都会自然地对电流流动产生一定程度的阻碍，这被称为阻抗（以欧姆为单位）。它包括“电阻”部分（对直流电流的阻碍）和“电抗”部分（对交流电流的阻碍）。在串联RLC电路中，其表示为：

Z = √R2 + (XL2 - XC2)

其中XL是感抗（电感器对交流电流的阻碍），XC是容抗（电容器对交流电压的阻碍）。

感抗和容抗均与频率相关，因此： 

• 当XL> XC时，电路中的总电抗变为电感性，电压领先电流90°相位角。 
• 当XL< XC时，电路变为电容性，电压滞后电流90°。  
• 当XL = XC时，电路变为谐振。这在电子电路中有许多重要应用。

并联RLC电路的特性

在并联RLC电路中，R、L和C元件上的电压保持不变，而流经每个元件的电流可能会发生变化。并联RLC电路的一些电气特性，与串联RLC电路是“倒数”关系；然而，其数学处理更具挑战性。

流经电路的总电流不等于流经每个元件的电流的代数和，而是其矢量和。

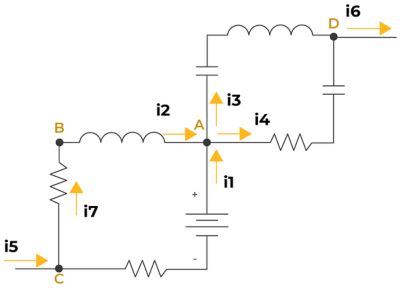
基尔霍夫电流定律（KCL）指出，流经电路中某一节点的电流之和等于零。因此，电路中任意节点处的源电流由以下公式给出：

IS - IR - IL - IC = 0

阻抗为：

1/Z = √(1/R)2 + (1/XL - 1/XC)2

值得注意的是，上述表达式是串联RLC电路中阻抗方程的倒数。事实上，由于电路中存在的对偶关系，并联RLC的属性与串联RLC的属性相互映照。因此，并联RLC的阻抗是串联RLC的对偶，表达式采用相同的一般形式。

阻抗（1/Z）的倒数称为导纳（以西门子为单位）。它为计算并联电路中的阻抗提供了更便捷的方法，尤其在涉及多个分支的情况下。并联电路中的总导纳就是各元件导纳之和。相反，在串联电路中，总阻抗是各元件阻抗之和。

值得一提的是，电阻（1/R）的倒数称为电导，而电抗（1/X）的倒数称为电纳。

串联和并联RLC电路之间的差异

如前所述，串联和并联配置的电路表达式互为倒数。这有助于电路设计人员确定，串联还是并联配置对于特定设计而言更方便。下表描述了串联和并联RLC电路之间的主要区别：

从根本上说，描述RLC电路行为的参数有两个，即谐振频率和阻尼系数。工程师可根据前两个参数导出其他参数，包括带宽和Q因子。

RLC电路中的谐振

RLC电路的一个重要特性是能够在特定频率（称为谐振频率）下谐振。物理系统具有自然频率，在这些频率下它们更容易振动。在谐振时（无论是否存在驱动源），振动会大幅增强，从而实现高效的能量转移。

在RLC电路中，电容器电场中储存的能量可以转移并储存到电感器周围的磁场中，反之亦然。这种转移可能会周期性地发生，从而导致RLC电路振荡。在谐振时，角频率ω（以弧度为单位）由以下公式给出：

ω = 1/√LC

此外，在谐振时，感抗等于容抗，电路的总阻抗（复数）为零。

因此，在串联RLC电路中，阻抗达到最小值，而在并联电路中达到最大值。 

了解和应用RLC电路中的谐振对于设计高效和有效的电子系统至关重要，尤其是在通信、电力系统和信号处理应用中。重要的谐振应用包括：

• 频率选择：在谐振时，RLC电路可以响应特定频率的信号，而排除其他频率，例如收音机中的调谐器。
• 滤波：RLC电路可以用作各种类型的滤波器，包括带通滤波器、带阻波器、低通滤波器或高通滤波器。此外，这些电路还可以用作集成电路中的噪声滤波器。它们还可以作为抑制器电路，抑制特定频率的电流，这种类型的并联电路被称为反谐振器。
• 电压倍增：如果电阻极小，电感器和电容器的电压可能比输入电压大几倍。这种电压倍增效应与电路的Q因子成正比。
• 阻抗匹配：在谐振时，串联RLC电路中的阻抗是纯电阻性的，并且达到最小值，而对于并联RLC电路，阻抗达到最大值。这可以用于阻抗匹配。
• 功率传输：由于串联RLC电路在谐振时达到最大功率传输，因此它们对于需要高效能量传输的应用至关重要。
• 振荡器电路：RLC电路通常用于振荡器应用，其中需要在特定频率下持续振荡。在这些情况下，电路的电阻最小化（对于串联电路）或最大化（对于并联电路），以减小阻尼并近似于理想的LC电路。

RLC电路中的阻尼

阻尼描述了振荡RLC系统中振荡幅度随时间而减小的趋势（由于电阻）。因此，在RLC电路能量耗散方面，电阻器发挥着至关重要的作用。它们还决定了电路是否会自然谐振（即在没有驱动源的情况下）。

因此，工程师会在RLC电路中观察到三种阻尼响应：

• 欠阻尼电路，其特征是振荡缓慢衰减
• 过阻尼电路，其中振荡会迅速停止
• 临界阻尼电路，振荡在达到稳态振荡所需的临界时间之前刚好停止
• 对于临界阻尼电路，\zeta = 1

无量纲阻尼比是帮助工程师表征RLC电路中的阻尼的重要参数。在振荡器电路中，工程师试图通过最小化串联电路中的电阻，同时最大化并联电路中的电阻，来最大限度地减小阻尼。在带通滤波器中，阻尼系数经过调整以匹配所需的带宽：值越大，带宽越宽，反之亦然。

RLC电路中的导出参数包括带宽和Q因子。

带宽

带宽描述了RLC电路谐振的频率范围。这是滤波器设计中的一个关键参数，其中，谐振附近阻抗的快速变化可用于通过或阻断接近谐振频率的信号，这一效应分别在带通滤波器和带阻波器中尤为明显。

带宽表示截止频率之间的频率间隙，通常定义为通过电路的功率是谐振时功率一半的频率。 

工程师可调整滤波器电路中的阻尼，以匹配所需的带宽。高阻尼会产生宽带滤波器。相反，低阻尼会产生窄带滤波器。

Q因子

无量纲Q因子描述了振荡系统的阻尼程度。其定义为，系统中储存的初始能量与振荡周期一个弧度内损失的能量之比。

Q因子越高，表示能量损失率越低，振荡衰减越慢（窄带、欠阻尼），而Q因子越低，表示网络损耗越大（宽带、过阻尼）。高Q值系统的示例包括时钟、激光器和音叉，后者的Q值在1000左右。一些高Q值激光器的Q值达到了1011或更高。

RLC电路集成了电阻器、电感器和电容器，是电路设计的支柱。利用电路的谐振和阻尼特性，工程师可以为一系列应用设计各种电路。因此，了解和表征RLC电路对于设计、分析和优化各种电子和通信系统的电路至关重要。

在RLC电路中，电磁耦合是影响这些电路性能的关键因素，其会影响频率响应、功率传输、阻尼和其他特性。

因此，在电路设计中，Ansys Exalto ®软件作为一款LVS后RLCk提取软件，通过提取集总元件寄生效应并生成准确的电气、磁和基板耦合模型，使设计人员能够准确地捕获设计层级中不同模块之间的串扰。Exalto软件可与大多数LVS软件包交互，并补充所选的RC提取工具。

此外，Ansys RaptorH ™软件是一款LVS前电磁建模软件，可对高速射频和数字SOC进行高容量电磁建模，包括电源网格、全定制模块、螺旋电感和时钟树。它将黄金标准的Ansys HFSS™电磁仿真引擎与芯片优化的Ansys RaptorX引擎相结合。

相关资源