-
United States -
United Kingdom -
India -
France -
Deutschland -
Italia -
日本 -
대한민국 -
中国 -
台灣
-
-
产品组合
查看所有产品Ansys致力于通过向学生提供免费的仿真工程软件来助力他们获得成功。
-
Ansys博客
January 23, 2024
什么是时域有限差分(FDTD)?
时域有限差分(FDTD)方法是一种3D全波电磁求解器,通常用于纳米光子器件、流程和材料的建模。
在光子学领域,FDTD已成为行业标准,而在高频电子领域,有限元法(FEM)和矩量法(MoM)则是主导性的黄金标准计算电磁求解器,它们各有其自身优势。本文重点介绍光子学仿真中的FDTD。
FDTD于1966年由Kane S. Yee首次提出,是一种求解James Clerk Maxwell变换方程(正式名称为Maxwell方程)的算法方法。这些方程于19世纪被构想出来,不仅统一了电学和磁学,而且还为无线电、电视和无线通信等技术奠定了基础。直到20世纪80年代,Yee的数值方法才被广泛称为“FDTD”。
Maxwell FDTD方程
Maxwell方程及其相关定律包括:
- 高斯电场定律:描述电荷如何产生电场
- 高斯磁定律:描述磁场没有孤立的磁极,即磁场线是闭合的。
- 法拉第感应定律:解释了变化的磁场如何在电路中感应出电磁力(EMF)
- 麦克斯韦-安培定律:将电流与磁场联系起来,并考虑了变化电场的作用。
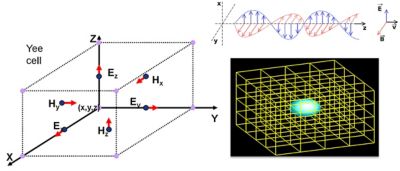
如上图所示,在FDTD中,每个场分量都在网格单元(Yee单元)中略微不同的位置求解。
FDTD的工作原理是什么?
在FDTD中,仿真域是由仿真区域截断并由网格离散化的空间。当运行FDTD仿真时,电磁(EM)场是根据每个网格单元中的Maxwell方程计算的,并对解进行重复的时间步进。空间离散化实现了对复杂的几何形状和结构的表示,而时间离散化则可以捕获电磁场随时间的演变。
FDTD有哪些应用?
FDTD方法通常适用于物体的部分或全部尺寸与光波长大小相当的设计情况。FDTD的准确性和通用性使其成为了各种光子设计的首选求解器,包括:
尽管FDTD是Maxwell方程最通用的求解方案,但更高效的方法也可应用于特定应用,例如最大限度地提高多层和衍射光学元件的设计灵活性。同样,光子集成元件的求解器组合策略也可用于更有效地处理不同的结构,例如用于波导结构的本征模展开(EME)方法。为正确的问题选择正确的求解器而构建战略方法,既能影响设计流程的速度和效率,也能影响结果的准确性。
FDTD方法广泛应用于纳米光子设计中。
FDTD的优势是什么?
利用FDTD,设计人员可以深入研究光的偏振以及光与不同材料和结构的波长相关相互作用。他们可以深入了解光学现象,例如反射、透射、衍射、干涉和吸收。
- 时域和频域分析:FDTD提供了电磁场随时间演变的动态视图。时域解决方案的内置自动傅里叶变换可轻松实现频率分析。
- 宽带功能:由于FDTD是一种时域方法,因此可通过单次仿真更快地计算出宽带结果。
- 复杂几何结构:FDTD在复杂几何结构建模方面表现出色,并且可以处理任意形状的结构。
- 准确性和通用性:该方法本质上不需要任何物理近似,因此具有高度的通用性和准确性。
FDTD的挑战是什么?
FDTD方法的高精度和通用性也带来了一些挑战,包括:
- 仿真尺寸:可准确建模的设备的最大物理尺寸最终受到可用计算资源的限制。
- 仿真时间:FDTD仿真的速度取决于多个因素,包括从仿真设置和体积到计算系统的硬件规格等。在3D仿真中,仿真时间预计按以下关系进行缩放:~V.(l/dx)4,其中V为仿真体积,dx为网格尺寸。因此,网格精度和设计尺寸会显著影响仿真时间。
- 内存和计算能力:FDTD仿真中,空间和时间未知数的绝对数量会随着网格的细化和仿真体积的增大而呈指数级增长。这就意味着,需要极大的内存和计算能力。
- 内存带宽:处理器之间的内存访问和大量数据交换,尤其是在处理大型仿真时, 是加速FDTD仿真的主要挑战。
如何加速FDTD仿真?
Ansys Lumerical利用多种先进方法来加速FDTD仿真。
微调算法
几十年来,Lumerical中的FDTD算法在基础层面进行了微调,以最大限度地减少计算开销,同时提供最高精度。Lumerical拥有多项专利和先进特性与功能,可帮助简化仿真设置,包括网格、监视器、光源、结构、材料、分析组等。内置的先进优化框架还可以加速优化纳米光子器件的生成。
并行计算
Ansys Lumerical FDTD具有高度优化的计算引擎,能够利用多核CPU计算系统,并在高性能计算(HPC)集群中利用图形处理单元(GPU)的并行架构。CPU和GPU架构在并行处理方面都表现出色,可满足FDTD仿真中的同步计算需求。HPC系统利用这种并行性来分配工作负载,从而显著提高仿真性能。大型仿真作业可以划分成多个独立的计算线程并行执行,从而在不到几小时的时间内完成500-1000亿个网格单元的大型仿真。
随着仿真复杂性的增加,对高效且可扩展计算资源的需求也在增加。这正是云计算和HPC的动态组合发挥作用的地方,其可彻底改变FDTD仿真。Lumerical解决方案提供了CPU和GPU兼容的仿真软件,用户可以在本地或云端进行部署。
如欲了解有关HPC和云端FDTD仿真软件的更多信息,请观看我们的网络研讨会“利用HPC和云计算加速光子设计”。
如欲了解有关基础求解器物理以及如何设置、运行和分析FDTD仿真的更多信息,请参阅Ansys创新课程(Ansys Innovation Courses)的FDTD学习板块。










