Was sind S-Parameter?

Streuparameter – auch S-Parameter genannt – bezeichnen Elemente in einer mathematischen Matrix, die das Verhalten eines elektrischen Netzes (oder Schaltkreises) beschreiben, wenn es durch ein elektrisches Signal stimuliert wird.

Bei hohen Frequenzen (mehr als einige Gigahertz) wird es schwierig, Spannungen und Ströme direkt zu messen. Daher beschreiben S-Parameter die Eingangs-/Ausgangsverhältnisse von Leistungswellen zwischen den Toren eines elektrischen Netzes.

In der Elektronik lassen sich S-Parameter auf eine Vielzahl von Schaltungen anwenden. Hierzu gehören unter anderem Kommunikationssysteme, integrierte Schaltkreise und Leiterplatten, Mikrowellenschaltkreise und Hochfrequenz-Schaltkreise (HF).

Insbesondere unterscheiden sich S-Parameter von anderen verwendeten Parametern wie Y-Parametern, Z-Parametern und ABCD-Parametern dadurch, dass sie angepasste Abschlüsse (statt Leerlauf- oder Kurzschlussabschlüssen) zur Charakterisierung elektrischer Netze verwenden.

Mathematische Ausdrücke helfen uns, die Welt um uns herum zu beschreiben. In elektrischen Kleinsignalnetzen setzen lineare Gleichungen unabhängige Größen von Spannungen und Strömen mit abhängigen Größen (ebenfalls Spannungen und Ströme) in Beziehung.

So lassen sich selbst die komplexesten Schaltkreise auf einfache „Black Boxes“ reduzieren, in denen die Ausgangsspannungen und -ströme durch einfache mathematische Beziehungen mit den Eingangsspannungen und -strömen in Beziehung gesetzt werden.

Vor dem Aufkommen von Schaltkreisen mit hoher Frequenz waren Y- und Z-Parameter die wichtigsten Methoden zur Charakterisierung der Netzleistung. Bei höheren Frequenzen wird es jedoch schwierig, die Netzleistung direkt mit Spannungen und Strömen in Beziehung zu setzen, insbesondere in Netzen, die Übertragungsleitungen wie Wellenleiter enthalten.

Daher beziehen sich S-Parameter auf die Elemente einer Streumatrix und beschreiben die Streumerkmale einer Spannungswelle, die sich durch ein elektrisches Netz oder einen Stromkreis ausbreitet. Sie stammen aus dem Streuwellenkonzept, das von E.W. Matthews, Kaneyuke Kurokawa und anderen breiteren Kreisen bekannt gemacht wurde.

Was sind Wanderwellen?

Wenn eine elektromagnetische Welle auf ein Hindernis trifft oder ein unterschiedliches Dielektrikum kreuzt, sagt man, dass sie „gestreut“ wird. So beschreiben S-Parameter, wie Ströme und Spannungen, die sich durch eine Übertragungsleitung ausbreiten, „gestreut“ werden, wenn sie auf eine durch eine Komponente oder ein Netz gebildete Störstelle treffen. Diese Störstelle ist auf eine Fehlanpassung der Komponente oder der Impedanz des Netzes an die Impedanz (oder Lastimpedanz) der Leitung zurückzuführen.

Wenn ein einfallendes Signal an einem Netztor ankommt, wird ein Teil seiner Energie vom Tor weg reflektiert, während der Rest zu den anderen Toren im Netz übertragen (oder gestreut) wird, was zu einer Verstärkung oder Dämpfung des Signals führt.

Berechnung von S-Parametern

Da S-Parameter die Merkmale von einfallenden und reflektierten Wellen bei bestimmten Frequenzen beschreiben, müssen diese Frequenzen zusammen mit den Wellenimpedanzen des Prüflings angegeben werden.

S-Parameter sind bei der Entwicklung, Analyse und Optimierung von Mikrowellen- und Hochfrequenzschaltkreisen (300 MHz bis 300 GHz) besonders nützlich (und werden dabei häufig verwendet). Sie machen es überflüssig, die internen Merkmale eines HF-Geräts zu modellieren, und ermöglichen es, sich nur auf das Eingangs-/Ausgangsverhalten zu konzentrieren.

S-Parameter werden von den an jedem Schaltkreistor gemessenen Spannungen und Strömen abgeleitet. Bei diesen Parametern handelt es sich um dimensionslose Koeffizienten, die als Spannungsverhältnisse von einfallenden und durchlaufenden (oder reflektierten) Wellen berechnet werden. Die Streumatrix für ein Mehrfaktor-Netz (n-Tor-Matrix) besteht aus 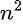  S-Parametern, wobei jeder Parameter einen Eingangs-/Ausgangspfad im Schaltkreis darstellt.

Jeder Parameter ist eine dimensionslose komplexe Zahl, wobei der reale Teil die Amplitude des Signals und der imaginäre Teil die Phase des Signals bei Prüffrequenz angibt. Die Amplitude kann entweder auf einer linearen oder logarithmischen Skala angegeben werden (in diesem Fall wird sie in Dezibel ausgedrückt). Die Phase wird normalerweise in Grad oder gelegentlich als Radiant ausgedrückt.

Es müssen außerdem folgende Bedingungen für die Messung der S-Parameter angegeben werden:

• Die Prüffrequenz
• Die Wellenimpedanz (normalerweise 50 Ω)
• Die Zuweisung von Tornummern
• Andere Bedingungen, wie z. B. der Vormagnetisierungsstrom, die Temperatur und die Steuerspannung

Darstellung von S-Parametern

S-Parameter werden als  Matrix angezeigt, wobei 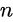 für das Eingangstor steht.

Daher wird die S-Matrix für ein Zweitor-Netz wie folgt geschrieben:

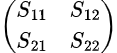
wobei:

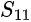•  der Reflexionsfaktor des Eingangstors ist
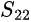•  der Reflexionsfaktor des Ausgangstors ist
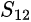•  der Transmissionsfaktor des Eingangstors (oder die „Verstärkung der Rückwärtsspannung“) ist
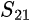•  der Transmissionsfaktor (oder die „Verstärkung der Durchlassspannung“) ist

Beachten Sie, dass diagonale Parameter als „Reflexionsfaktoren“ bezeichnet werden, da Signaleingänge und -ausgänge an einem einzigen Tor stattfinden, während nicht diagonale Parameter als „Transmissionsfaktoren“ bezeichnet werden, die Eingänge und Ausgänge an verschiedenen Toren anzeigen. Das ist für jede Matrix 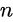-ter Ordnung ähnlich.

S-Parameter können auf einem Linear- oder Polardiagramm dargestellt werden, in dem jeder Punkt eine Prüffrequenz darstellt.

S-Parameter in der Auslegung von HF-Schaltkreisen

S-Parameter werden in der Elektronik gemessen, um Merkmale wie Verlust, Verstärkung, Impedanz und Stehwellenverhältnis (VSWR) in einem linearen Netzwerk mit hoher Frequenz (HF oder Mikrowellen) zu bestimmen. Verschiedene elektrische Standards, einschließlich 10 GbE, SATA, PCIe und Glasfaserkanäle, beschreiben ihre Verfahren für die Prüfungskonformität mit Hilfe von S-Parametern.

Zu den wichtigsten Anwendungen gehören:

• Verstärkerkonzept: Bei der Auslegung von HF-Verstärkern werden Verstärkung, Stabilität und Linearität mit Hilfe von S-Parametern analysiert, um eine maximale Bandbreite sowie optimale Anpassungsergebnisse der Ein- und Ausgänge zu erzielen.
• Filterdesign: S-Parameter helfen die Frequenzantwort, die Einfügedämpfung, die Rückflussdämpfung und die Trennschärfe bei Hochpass-, Bandpass-, Tiefpassfiltern und Bandsperren zu beurteilen.
• Charakterisierung der Frequenzantwort: Da S-Parameter je nach angelegter Frequenz variieren, können sie die charakteristischen Antworten von HF-Schaltkreisen über einen breiten Frequenzbereich deutlich machen, was die Charakterisierung von Bandbreite, Resonanz, parasitären Einflüssen und anderen frequenzabhängigen Antworten ermöglicht.
  
• Charakterisierung der Übertragungsantwort: S-Parameter machen deutlich, wie gut HF-Schaltkreise Energie zwischen Toren übertragen, und charakterisieren Antworten bei Verlust, Verstärkung und Phasenverschiebung.
  
• Impedanzanpassung: Durch die Untersuchung von S-Parametern (insbesondere Reflexionsfaktoren) lässt sich eine optimale Impedanzanpassung zwischen Schaltkreiskomponenten erzielen und die Leistungsübertragung zwischen Quellen und Lasten maximieren.
  
• Verbindungsanalyse: S-Parameter helfen bei der Charakterisierung von Nebensprechen, Signalintegrität, Impedanzfehlanpassung und anderen Effekten in Verbindungen und Übertragungsleitungen.
  
• Signal-Integritäts-Analyse: Die Signalleistung kann durch Dämpfung, Reflexionen und Impedanzfehlanpassungen negativ beeinflusst werden, was sich durch Untersuchung der S-Parameter in einem Netz begrenzen lässt.
• Auslegung von Schaltkreisen: Zur Bewertung verschiedener HF-Schaltkreiskonfigurationen werden S-Parameter verwendet, um die Spezifikationen für Verstärkung, Verlust, Leistungsübertragung und Impedanzanpassung zu optimieren.
• Netzanalyse: Die Leistung komplexer Netze (wie Phasenverschiebung, Verstärkung und Frequenzantwort) lassen sich analysieren, indem sie die S-Parameter einzelner Komponenten hintereinanderschalten.

S-Parameter liefern wertvolle Informationen über die Leistung linearer elektrischer Netze, einschließlich von HF-Schaltkreisen, Verstärkern und Filtern. Diese Informationen umfassen:

• Details zu Größe, Phase, Reflexion und Dämpfung von Signalen
• Orte von Signalverlusten und Impedanzfehlanpassungen
• Übertragungsleitungsparameter, wie R, L, C, G, TD und Z0

Außerdem sind S-Parameter bei HF-Frequenzen einfacher zu messen als Y- oder Z-Parameter, da sie keinen Leerlauf oder Kurzschlüsse erfordern. Sie können auch einfach in andere Parameterformate konvertiert werden, darunter ABCD-Parameter, H-Parameter, T-Parameter, Y-Parameter und Z-Parameter, so dass sie Flexibilität bei der Analyse und der Auslegung von Schaltkreisen bieten.

S-Parameter können auch einfach als Touchstone-Dateien (ASCII-Textdateien) gespeichert werden, die von der Schaltkreis-Simulationssoftware gelesen werden können.

Die Verwendung von S-Parametern hat zwar viele Vorteile, es gibt jedoch einige wenige Einschränkungen:

• S-Parameter können nur in der Frequenzbereichsanalyse (Frequenzantwort von Signalen), aber nicht in der Zeitbereichsanalyse (Einschwingverhalten von Signalen) verwendet werden.
• Bei Verwendung von S-Parametern ist es nicht möglich, Netze gleichzeitig nach Spannungs- und Stromwellen zu charakterisieren. Dazu werden ABCD-Parameter verwendet. Außerdem ist es einfacher, ABCD-Parameter hintereinander zu schalten als S-Parameter.
• Die meisten Siliziumlasten verhalten sich nichtlinear.

Digitale Schaltkreise werden weitgehend von Spannungsschwellen bestimmt, bei denen es gilt, den Fluss der elektrischen Energie zu verstehen. Hierzu ist wiederum eine Zeitbereichsanalyse erforderlich. Die Zeitbereichsanalyse ist auch bei der Auslegung von Schaltkreisen mit Antennen wichtig, bei denen Ingenieur*innen Reflexionen und Streusignale charakterisieren müssen.

Die Frequenzbereichsanalyse vereinfacht die mathematische Analyse und bietet ein intuitives Verständnis der Systemqualität. Diese wird mit Begriffen wie Verstärkung, Bandbreite, Resonanzfrequenz und Phasenverschiebung beschrieben, wenn es um die zeitabhängigen Elemente der Frequenzmerkmale geht. 

Außerdem können Signalinformationen zwischen Frequenz- und Zeitbereichen mithilfe mathematischer Operatoren, die Transformationen genannt werden (z. B. Fourier-Transformationen), umgewandelt werden, obwohl dies zu Fehlern führen kann.

Im Matrixmodell stellt eine „Black Box“ ein elektrisches Netz dar, das Verbindungskomponenten wie Transistoren, Kondensatoren, Widerstände und Induktoren enthält, die über verschiedene Tore mit anderen Stromkreisen interagieren.

Das Netz kann eine beliebige Anzahl an Komponenten enthalten, vorausgesetzt, es verhält sich bei Anlegen kleiner Störsignale linear. Es kann auch in Kommunikationssystemen typische Komponenten wie Dämpfungsglieder, Verstärker, Koppler und Filter enthalten, sofern auch diese linear arbeiten.

Kleinsignal-S-Parameter

In der überwiegenden Mehrheit der Fälle gelten S-Parameter für Einzelfrequenz-Kleinsignalnetze. In diesen Netzen ist das Signal so klein, dass die Kompression der Verstärkung oder andere nichtlineare Effekte vernachlässigbar sind. Daher werden Kleinsignal-S-Parameter einfach als Spannungsverhältnisse von reflektierten und einfallenden Wellen berechnet.

Lineare Netze umfassen:

• Verlustfreie Netze, die keine Leistung abgeben, sodass die Summe der einfallenden Leistungen der Summe der reflektierten Leistungen über alle Tore hinweg entspricht. Dies bedeutet, dass die S-Parameter-Matrix unitär ist.
• Verlustbehaftete passive Netze, in denen die Summe der einfallenden Leistungen die Summe der ausgehenden Leistungen übersteigt, was bedeutet, dass das Netz Energie abgibt.
• Reziproke passive Netze, die ausschließlich aus reziproken Materialien bestehen, die das übertragene Signal beeinflussen. Kabel, Splitter, Dämpfungsglieder und Kombinatoren sind Beispiele für reziproke Netze. In diesem Fall ist die S-Parameter-Matrix gleich ihrer Transponierten, so dass 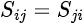 ist
  
  

Großsignal-S-Parameter

Mit zunehmender Stärke des Eingangssignals werden nichtlineare Effekte wie die Kompression der Verstärkung spürbar. Daher variieren Großsignal-S-Parameter je nach Eingangsleistungspegel. Diese werden auch als „leistungsabhängige S-Parameter“ bezeichnet.

Messungen von Großsignal-S-Parametern stützen sich auf eine Harmonic Balance-Simulation des Netzes. Diese Methode zur Frequenzbereichsanalyse wird auf nichtlineare Schaltkreise angewendet. Großsignal-S-Parameter werden auch als Spannungsverhältnisse von reflektierten und einfallenden Wellen berechnet.

Gemischte S-Parameter

Häufig müssen S-Parameter-Berechnungen anhand von Frequenz- und Verstärkungsdiagrammen oder Smith-Diagrammen verglichen werden. Daher werden gemischte S-Parameter graphisch dargestellt. Diese Parameter werden zur Charakterisierung von Nahnebensprechen (NEXT) und Fernnebensprechen (FEXT) in differenzierenden Netzen verwendet.

Zweitor-S-Parameter

In der Regel werden in der Netzanalyse Zweitor-S-Parameter verwendet, die auch als Vorlage für S-Parameter-Matrizen höherer Ordnung in größeren Netzen dienen. Die Beziehung zwischen reflektierten und einfallenden Wellen in Zweitor-Netzen ergibt sich aus:

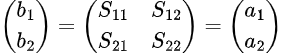
wobei 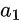 und 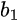die Amplituden der einfallenden und reflektierten Wellen an Tor 1 und ähnlich für  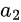und 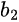an Tor 2 sind.

Aus Messungen von Zweitor-S-Parametern werden die folgenden Netzeigenschaften abgeleitet:

• Einfügedämpfung
• Eingangsrückflussdämpfung
• Ausgangsrückflussdämpfung
• Skalare lineare Verstärkung
• Komplexe lineare Verstärkung
• Skalare logarithmische Verstärkung
• Rückwärtsverstärkung und Rückwärtsisolierung
• Reflexionsfaktor
• Stehwellenverhältnis

Wie bereits erwähnt, helfen S-Parameter bei der Beschreibung des Ansprechverhaltens eines allgemeinen elektrischen 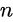-Tor-Netzes, in dem Signale an einem beliebigen Tor angelegt und reflektiert werden. Daher beschreibt ein Parameter  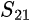eine Netzantwort an Tor 2 eines an Tor 1 einfallenden Signals. S-Parameter werden häufig auf Ein- und Zweitor-Netze angewendet.

Messungen von Dreitor-S-Parametern stellen eine größere Herausforderung dar, obwohl sie sich mit spezieller Software modellieren lassen. Auch Messungen von Mehrfachtor-S-Parametern sind bei Geräteherstellern erhältlich, aber diese Messungen müssen immer auf ihre Genauigkeit überprüft werden.

Verwenden von vektoriellen Netzwerkanalysatoren (VNA)

Zur Untersuchung der Signalintegrität werden regelmäßig vektorielle Netzwerkanalysatoren verwendet, um die Leistung von HF- und Mikrowellenschaltkreisen unter verschiedentlichen Betriebsbedingungen zu bewerten. Daher werden häufig eine signifikante Menge an S-Parameterdaten herausgerechnet, kaskadiert und visualisiert, wobei eine Kombination aus theoretischer Analyse und Experimenten durchgeführt wird. Der Prozess umfasst in der Regel:

• Eine theoretische Analyse des Schaltkreismodells oder Schaltplans unter Anwendung der elektromagnetischen Theorie, der Leitungstheorie und der Netzwerktheorie, um mathematische Gleichungen abzuleiten
• Eine Simulation des Schaltkreisverhaltens mit Hilfe einer speziellen Software (auf Grundlage der abgeleiteten Gleichungen) zur Extraktion von S-Parametern
• Experimente mit einem vektoriellen Netzwerkanalysator zur Extraktion von S-Parameterwerten über einen Frequenzbereich
  
• Ggf. Herausrechnen (Subtrahieren) der S-Parameter-Anteile einzelner Komponenten aus einem Stromkreis
  

Während der Prüfung wird ein bekanntes Signal von einer VNA-Quelle in den Prüfling geschickt, um Änderungen am Signal während der Durchquerung des Prüflings zu messen. Diese Änderungen werden von einem Empfänger (oder einer Gruppe von Empfängern) erfasst, der mit dem VNA verbunden ist.

Eine typische VNA-Einrichtung umfasst:

• Einen Ablenkungsoszillator (normalerweise ein Synthesizer)
• Ein Informationsdisplay
• Zwei oder mehr Tore (oft verbunden mit Doppel-Richtkopplern und einem Messgerät für komplexe Verhältnisse)
• HF-Kabel

Optional kann eine Vorrichtung zur Steuerung von Vorspannung oder Vormagnetisierungsstrom oder eine Steuerung zum Speichern von Daten enthalten sein.

Ein vektorieller Netzwerkanalysator erfasst die Frequenzantworten einer einzelnen Komponente (oder einer Gruppe von Komponenten, entweder passiv oder aktiv) in einem HF-Netz. Er misst die Leistung eines bestimmten Signals und erfasst dessen Phase und Amplitude.

Aus diesen Amplituden- und Phasenmessungen lassen sich eine Reihe von Gerätemerkmalen ableiten, einschließlich Gruppenlaufzeit, Impedanz, Rückfluss und Einfügedämpfung.

VNA sind Ein- oder Mehrwege-Instrumente mit mehreren Toren, bei denen an jedem der Tore Reize angelegt werden können, z. B.:

• Ein Zweitor-Einwege-VNA gibt reflektierte und übertragene Signalwerte am Eingangstor 1 ( 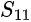bzw. 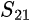) zurück. Der Prüfling muss jedoch umgekehrt werden, um die entgegengesetzten Parameter an Tor 2 ( 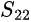und 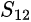) zu erhalten.
• Ein Zweitor-VNA kann den Signalfluss auch umkehren, d. h. Messungen können in beide Richtungen durchgeführt werden, um die Reflexions- und Transmissionsfaktoren an jedem Tor zu extrahieren.

Darüber hinaus beeinflusst die Position der Bezugsebene, auf der Kalibrierungen durchgeführt werden, die VNA-Messungen.

Messfehler

Ursachen für Messfehler sind u. a.:

• Schwankungen der Frequenzantworten, die durch leichte Schwankungen der Frequenzantworten der Empfänger des VNA verursacht werden
• Schwankungen der Torimpedanzen, die durch leichte Unterschiede zwischen der charakteristischen Bezugsimpedanz und der Eingangsimpedanz am Prüftor verursacht werden
• Richtungsfehler, bei denen Teile von einfallenden und reflektierten Wellen aufeinander treffen und die Messungen in beiden Richtungen beeinflussen
  
• Fehler der Isolierung, bei denen ein kleiner Teil des einfallenden Signals an einem Tor in den Empfängerkanal eines anderen Tors eindringen kann, was zu Nebensprechen führt.
  

Visualisieren von S-Parametern

Die Visualisierung ist ein wichtiger erster Schritt bei der Analyse von S-Parameterdaten. Phasen- und Amplitudendaten können entweder in kartesischen oder polaren Koordinatensystemen dargestellt werden. Ein Smith-Diagramm ist ein Polardiagramm, das zur Analyse von Anpassungsnetzwerken verwendet wird.

Für die genaue Durchführung von S-Parameter-Berechnungen sind fundierte Kenntnisse der HF-Schaltkreistheorie, Erfahrung mit Simulationssoftware und der Zugriff auf zuverlässige Ausrüstung erforderlich.

Das Auslegen von HF-Schaltkreisen ist eine komplexe Aufgabe, die mehrere Iterationen umfasst. Die Genauigkeit und Komplexität des Schaltkreises und die verfügbaren Tools bestimmen den Ansatz.

Im Folgenden werden die Schritte in einem typischen Ansatz zur Auslegung von S-Parametern in einem HF-Schaltkreis mit hoher Frequenz beschrieben:

• Schaltkreis-Layout: Beim Auslegen des Schaltkreis-Layouts wird die Topologie von Schaltkreiskomponenten, Übertragungsleitungen und Verbindungen berücksichtigt. Zudem müssen dabei Impedanzanpassung und Signalintegrität beachtet werden.
• Komponentenauswahl: Verstärker, Mischer, Filter und andere Komponenten werden je nach Anforderungen so zusammengestellt, dass sich die Merkmale Verstärkung, Leistungsumschlag, Frequenzantwort usw. ausgleichen.
• Simulation und Optimierung: Schaltkreismodell, Verbindungen und Komponenteneigenschaften sowie andere Parameter werden in einem speziellen Softwaretool programmiert, um simulierte S-Parameterwerte zu erhalten. Anschließend werden die Eingänge (z. B. die Länge der Übertragungsleitungen) so eingestellt, dass optimale S-Parameterwerte für Bandbreite, Verstärkung, Impedanzanpassung usw. erreicht werden.
  
• Prototypenerstellung: Sobald man die gewünschten Parameter erhalten hat, erstellt man mit einem vektoriellen Netzwerkanalysator einen Schaltkreisprototyp, um die tatsächlichen S-Parameterwerte zu messen.
• Validierung: Als abschließenden Schritt des Prozesses können die VNA-S-Parameterwerte mit simulierten Werten verglichen werden. Eventuelle Abweichungen werden durch Verfeinerung des Schaltkreislayouts und der Komponentenauswahl immer wieder ausgeglichen, bis die gemessenen und simulierten S-Matrizen übereinstimmen.
  

Der Wechsel von der parallelen zur seriellen Hochgeschwindigkeits-Datenübertragung führt zu einer Reihe neuer Herausforderungen bei der Halbleiterkonstruktion. Da die Datenraten Gigabit pro Sekunde immer näher kommen und so mehr Bits durch jede Verbindung schieben, werden mehrere serielle Verbindungen benötigt, die parallel arbeiten, was zu Verlusten bei Verbindungen mit hoher Frequenz führt und das Nebensprechen steigert.

Daher ist es wichtig, die elektromagnetische Kopplung in Halbleiterchips zu charakterisieren.

Ansys Ansys RaptorH™ elektromagnetische (EM) Modellierungssoftware wurde für die optimale Konfiguration von Halbleiterschaltkreisen entwickelt und kombiniert die Engine von Ansys HFSS™ mit der Software Ansys RaptorH in einem praktischen Paket.

Die schnelle verteilte Verarbeitung der RaptorH Software wird von allen wichtigen Siliziumfertigungsbetrieben unterstützt und ermöglicht präzise, siliziumbewährte S-Parameter- und RLCk-Modellierung in wenigen Minuten. Weitere Informationen finden Sie auf der dedizierten Seite der Software Ansys RaptorH.

∑_(i=1)^n I_i=0

Zugehörige Ressourcen