Che cos'è il flusso di un fluido?

Il flusso di un fluido descrive la deformazione continua e il movimento di liquidi o gas in risposta alle forze applicate o alle differenze di pressione. Il flusso di un fluido riflette la capacità del fluido di cambiare forma o adattarsi al suo contenitore, a differenza dei solidi, che mantengono una forma fissa.

Il comportamento dei fluidi durante il flusso è influenzato dalla loro viscosità, che misura la resistenza interna del fluido al flusso. In base alle loro caratteristiche di viscosità, i fluidi sono classificati come newtoniani o non newtoniani.

La comprensione del flusso di un fluido è fondamentale in molti campi ingegneristici, tra cui quella aerospaziale, civile, meccanica e biomedica. Svolge anche un ruolo significativo in discipline scientifiche come l'oceanografia, la meteorologia e la biologia. Per risolvere problemi complessi di flusso di un fluido, gli ingegneri spesso utilizzano tecniche avanzate come la fluidodinamica computazionale (CFD), che combina un potente hardware di elaborazione con sofisticati metodi numerici.

La meccanica dei fluidi è lo studio di liquidi e gas in movimento basato sulle leggi empiriche derivate dalle misurazioni del flusso. I problemi di flusso di un fluido in genere implicano la determinazione di proprietà quali:

• Velocità del fluido: una quantità vettoriale che descrive la velocità e la direzione in cui il fluido si muove (in metri al secondo)
• Pressione del fluido: una quantità vettoriale che descrive la forza per unità di area esercitata da un fluido sull'ambiente circostante o su una superficie con cui interagisce (in pascal o libbre per pollice quadrato)
• Temperatura del fluido: rappresenta l'energia cinetica media delle molecole all'interno di un fluido, che riflette quanto caldo o freddo è il fluido (in gradi Celsius, Kelvin o Fahrenheit) 
• Viscosità del fluido: misura della resistenza di un fluido al flusso e alla deformazione, quantifica l'attrito interno tra gli strati adiacenti del fluido mentre si muovono l'uno rispetto all'altro (in pascal-secondi)

Esistono molte sottodiscipline della meccanica dei fluidi, tra cui l'aerodinamica (si occupa dello studio dell'aria e dei gas in movimento, come il calcolo delle forze sulle ali degli aerei) e l'idrodinamica (si occupa dello studio del liquido in movimento, come la determinazione della portata del fluido di massa attraverso le condutture).

Il numero di Reynolds nel flusso di un fluido

Gli ingegneri utilizzano spesso numeri senza dimensioni per ridurre efficacemente il numero di variabili ed estrarre correlazioni significative da fenomeni fisici. Il numero di Reynolds è uno di questi numeri e mette in relazione le forze inerziali alle forze viscose nel flusso di un fluido.

Nel flusso laminare, le forze viscose sono maggiori rispetto alle forze inerziali. Con un numero di Reynolds crescente, le forze inerziali diventano più dominanti fino a quando il flusso diventa turbolento. Il numero di Reynolds al quale ciò avviene è noto come numero critico di Reynolds.

Il numero critico di Reynolds non ha un valore fisso, ma dipende da fattori quali l'uniformità delle superfici di delimitazione e la geometria del flusso. Ad esempio, per i flussi interni delimitati da una superficie liscia, il suo valore è di circa 2.300, mentre per i flussi esterni può essere molto più alto.

I flussi di fluidi assumono molti attributi, che riflettono le proprietà intrinseche del fluido o il modo in cui cambia nello spazio e nel tempo. Inoltre, i flussi turbolenti presentano ulteriori sfide. Ad oggi, i ricercatori devono ancora fornire soluzioni eleganti a questi problemi.

Il flusso laminare descrive i flussi in cui non vi è alcuna miscelazione tra i diversi strati di fluido (lamina) in un flusso. I flussi laminari si verificano quando le forze viscose sono più forti delle forze inerziali. La maggior parte dei flussi naturali di interesse ingegneristico, tuttavia, si trasforma in turbolenza.

Nei flussi turbolenti, gli strati di fluido si mescolano, dando luogo a sollecitazioni che formano elementi rotanti (ricircolo e curve). Il flusso turbolento si verifica quando le forze inerziali sono più forti delle forze viscose.

Vale la pena notare che esiste un terzo tipo di flusso, un flusso transitorio, che non è completamente turbolento né laminare.

Gli ingegneri studiano i flussi turbolenti attraverso una decomposizione di Reynolds, in cui il flusso viene separato in un componente medio e in un componente perturbativo. Il numero di Reynolds è definito come il rapporto tra forze inerziali e forze viscose all'interno di un fluido. Si tratta di una quantità senza dimensioni che aiuta a determinare se un flusso sarà laminare o turbolento per una determinata configurazione. È dato dalla:

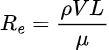
Dove ρ è la densità del fluido, V è la velocità del flusso e L è una lunghezza caratteristica (come il diametro di un tubo).

Ad esempio, si considerino tubi che hanno le caratteristiche seguenti:

• Se R_e è inferiore a 2.000, le forze viscose dominano e il regime di flusso è laminare.
• Se R_e è maggiore di 4.000, le forze inerziali dominano e il regime di flusso è turbolento.
• Se R_e è compreso tra 2.000 e 4.000, il flusso è transitorio.

Di seguito sono riportate le principali differenze tra flussi laminari e turbolenti:

Flusso stazionario e flusso non stazionario

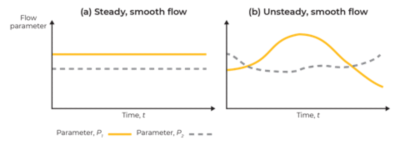
Un flusso stazionario è un flusso in cui le proprietà come velocità, pressione e densità non cambiano con il tempo in un dato punto nello spazio. Al contrario, se una di queste proprietà cambia con il tempo, il flusso è non stazionario.

I flussi turbolenti sono, per natura, non stazionari. Tuttavia, possono anche essere statisticamente stazionari, il che significa che le condizioni di flusso mediate nel tempo, come la velocità, rimangono costanti nel tempo.

I flussi non stazionari si trovano comunemente in natura. Tuttavia, i modelli di flusso non stazionari sono più difficili da risolvere perché l'introduzione della dimensione temporale richiede una capacità computazionale notevolmente maggiore.

Flusso uniforme e non uniforme

Il flusso uniforme descrive il flusso del fluido in cui la velocità del fluido rimane costante nella direzione e nella grandezza attraverso il flusso.

Flusso comprimibile e flusso incomprimibile

La compressibilità descrive la capacità di avvicinare le molecole di un fluido. 

I gas sono facili da comprimere perché le loro molecole sono molto distanti. Il loro volume e la loro densità possono essere modificati facilmente applicando o allentando la pressione. D'altra parte, i liquidi sono difficili da comprimere perché le loro molecole sono molto più vicine l'una all'altra. 

Per la maggior parte delle applicazioni pratiche, i liquidi possono essere considerati incomprimibili (tranne nei casi in cui la propagazione del suono diventa significativa, come in alcuni problemi di flusso non stazionario).

Nei campi di flusso in cui le variazioni di velocità sono piccole rispetto alla velocità del suono in quel fluido, il flusso di fluidi può essere trattato come incomprimibile (anche per i gas). Ciò è significativo perché gli effetti di compressibilità aumentano considerevolmente la complessità delle equazioni che lo regolano.

Il numero di Mach è un utile numero senza dimensioni che aiuta a determinare il significato degli effetti di compressibilità nel flusso di fluidi. Per numeri di Mach inferiori o uguali a 0,3 il flusso può essere considerato incomprimibile. Per velocità di flusso più elevate (supersoniche e supersoniche elevate), gli effetti di compressibilità diventano significativi, specialmente quando sono coinvolte onde d'urto, ad esempio nei motori a reazione, negli aerei ad alta velocità e nei razzi.

Flusso viscoso e flusso non viscoso

La viscosità è una misura dell'attrito in un fluido. Quando gli strati all'interno di un fluido sfregano l'uno contro l'altro, c'è attrito. L'elevata viscosità (ad esempio, il miele) indica un elevato attrito e viceversa. Per un liquido, la viscosità diminuisce con l'aumentare della temperatura. Questo perché le molecole si muovono più liberamente in un liquido più caldo e possono scivolare più facilmente l'una sull'altra. Per un gas, tuttavia, la viscosità aumenta con la temperatura.

Flusso singolo e multidimensionale

La dimensionalità del flusso indica il numero di dimensioni spaziali che influenzano in modo significativo le caratteristiche di un flusso; il tempo viene spesso indicato come una dimensione.

Nei flussi unidimensionali, quantità come velocità, pressione e densità variano significativamente in una sola dimensione. I modelli di flusso unidimensionali sono utili in condizioni di flusso in cui le variazioni nelle altre due dimensioni sono trascurabili (ad esempio, in un tubo con diametro costante in cui si verificano variazioni solo lungo la lunghezza del tubo).

Nei modelli di flusso bidimensionali, le variazioni nella terza dimensione sono uniformi o trascurabili. Ciò si verifica nei flussi con un rapporto d'aspetto elevato, in cui una dimensione è considerevolmente più grande dell'altra. Ad esempio, nello sviluppo dello strato di delimitazione lungo una piastra piatta, le variazioni nelle proprietà di flusso lungo la larghezza della piastra sono trascurabili rispetto alle variazioni lungo la lunghezza e l'altezza. Inoltre, molti modelli di sistema meteorologico sono bidimensionali perché l'atmosfera della Terra è molto sottile rispetto alla superficie della Terra.

I modelli di flusso tridimensionali sono i più diffusi nelle applicazioni ingegneristiche e catturano l'intera complessità di questi flussi in tre dimensioni. In questi casi, geometrie complesse creano intricati movimenti di fluidi che sono anche influenzati da variazioni tridimensionali di quantità come pressione, velocità o densità.

Sebbene i modelli unidimensionali e bidimensionali semplificati consentano di ridurre lo sforzo analitico, non sempre sono un'opzione valida. La scelta del modello dipende dal problema in esame. Gli ingegneri spesso si affidano a modelli semplificati nelle fasi iniziali della progettazione, optando per la modellazione 3D avanzata nelle fasi di verifica finale.

Flusso esterno e interno

Le principali differenze tra flussi esterni e interni derivano dalla natura dei confini che circondano tali flussi.

I flussi esterni si verificano quando almeno un lato non è delimitato, causando uno strato di delimitazione ed effetti scia. D'altra parte, i flussi interni si verificano all'interno di confini delimitati (solidi), in cui le cadute di pressione e le distribuzioni del flusso sono spesso d'interesse.

Esempi di flussi esterni includono il flusso d'aria sulla fusoliera di un aeromobile (in cui le forze aerodinamiche come il sollevamento e la resistenza sono spesso d'interesse), l'acqua che scorre lungo lo scafo di una nave o il vento che soffia su un edificio. La forma e l'orientamento degli oggetti influenzano i comportamenti di flussi esterni, formando strati di delimitazione (regioni viscose nelle interfacce oggetto-flusso) e separazioni di flusso.

Esempi di flussi interni includono l'aria o l'acqua che scorre attraverso tubi o condotti. Sono confinati dalle pareti di delimitazione e la quantità di moto persa verso le pareti determina un calo di pressione lungo la direzione del flusso.

Flusso multifase

Un flusso multifase descrive un flusso che incorpora la presenza simultanea di due o più fasi termodinamiche distinte. Queste fasi possono assumere la forma di gas, liquidi o solidi ed essere dello stesso o di componenti diversi, come il flusso acqua/vapore acqueo, il flusso olio/acqua o le sospensioni liquido-solido.

I flussi multifase sono generalmente classificati in flussi bifase e trifase, sebbene i sistemi più complessi possano includere fasi aggiuntive.

I flussi a due fasi comuni includono:

• Flussi gas-liquido: sono presenti negli evaporatori e nei condensatori
• Flussi gas-solido: sono presenti nei bioreattori
• Flussi liquido-solido: sono presenti nei sistemi di trasporto e sedimentazione dei liquami

I flussi trifase includono flussi gas-liquido-solido (come nei reattori chimici e nei letti fluidizzati) e flussi gas-liquido-liquido (che si trovano nei sistemi di recupero del petrolio).

La modellazione del flusso multifase è complessa a causa dell'interazione tra fasi diverse. È fondamentale per una serie di problemi ingegneristici, tra cui la lavorazione chimica e farmaceutica (ad esempio, miscelazione, filtrazione e separazione), la generazione di energia (turbine a vapore e modellazione della combustione) e petrolio e gas (riduzione del flaring e della ventilazione). Per risolvere questi problemi, gli ingegneri utilizzano approcci come i metodi Euler-Lagrange, Euler-Euler o VOF (volume of fluid).

La simulazione numerica diretta (DNS) di flussi turbolenti basata sulle equazioni di Navier-Stokes (escludendo la modellazione della turbolenza) è possibile con numeri di Reynolds moderati. Tuttavia, a causa delle eccessive risorse computazionali richieste, la maggior parte dei flussi ingegneristici mostra numeri di Reynolds troppo alti per la simulazione numerica diretta. Ad esempio, qualsiasi velivolo abbastanza grande da trasportare un essere umano non è alla portata della DNS (Re = 4 milioni).

Pertanto, gli ingegneri combinano le equazioni RANS (Reynolds-averaged Navier-Stokes) con la modellazione della turbolenza per fornire una caratterizzazione efficace di flussi turbolenti. I modelli RANS tengono conto del momento aggiuntivo e del trasferimento di calore causato dalla turbolenza attraverso le sollecitazioni di Reynolds. I modelli RANS sono ampiamente utilizzati nelle applicazioni ingegneristiche perché sono computazionalmente meno intensivi della DNS, fornendo al contempo una precisione ragionevole per molti tipi di flussi turbolenti.

Le simulazioni parassite di grandi dimensioni (LES) e le sue varianti sono altri approcci di modellazione che forniscono una via di mezzo tra DNS e RANS. La LES risolve direttamente le scale di turbolenza più grandi e modella le scale più piccole, rendendole più accurate rispetto a RANS. È un elemento fondamentale quando si cerca di modellare flussi in cui la transitorietà è importante, come l'aerodinamica esterna delle automobili e la combustione all'interno dei motori a turbina a gas. 

La capacità di comprendere il flusso di un fluido rappresenta il primo passo per sviluppare modelli computazionali efficaci. Le soluzioni di flusso laminare sono relativamente semplici e gli ingegneri possono utilizzare modelli matematici deterministici. Tuttavia, la gamma di applicabilità di questi modelli è limitata. 

La maggior parte dei problemi pratici riguardano flussi turbolenti, che sono i più difficili da modellare a causa della loro natura non stazionaria e non deterministica. La modellazione accurata di flussi turbolenti rimane una sfida che gli ingegneri stanno ancora cercando di risolvere.

Tuttavia, il software Ansys Fluent è lo strumento di simulazione di fluidi leader del settore noto per le sue capacità avanzate di modellazione fisica e la precisione senza pari.

Il software Fluent è uno strumento potente per gli ingegneri, che offre soluzioni efficienti e accurate per problemi di simulazione di fluidi complessi. Fornisce un'ampia gamma di modelli fisici e tecniche, tra cui:

• Una vasta gamma di modelli di turbolenza 
• Modellazione a ordine ridotto
• Una vasta gamma di modelli di flusso multifase
• Numerosi modelli a combustione
• Interazioni fluido-struttura
• Funzionalità parallele altamente scalabili per mesh e risoluzione

Risorse correlate