INFORMATIONS SUR LE SUJET
- Qu'est-ce que la mécanique des fluides numériques (CFD) ?
- Exemples de la mécanique des fluides numériques
- Fonctionnement de la dynamique des fluides numériques
- Défis de la modélisation de l'écoulement des fluides
- Histoire de la dynamique des fluides numériques
- Équations principales de CFD
- Avancées en matière de CFD
Qu'est-ce que la mécanique des fluides numériques (CFD) ?
La mécanique des fluides numériques (CFD) est la science qui consiste à utiliser des ordinateurs pour prédire les écoulements de liquides et de gaz sur la base des équations principales de conservation de la masse, de la quantité de mouvement et de l'énergie. Les fluides sont tout autour de nous et régissent nos vies de différentes façons. Les vibrations dans vos cordes vocales génèrent des ondes de pression dans l'air qui rendent la parole possible, ainsi que l'audition des mots prononcés. Sans fluides, la frappe de votre balle de tennis ne serait rien, et votre avion n'aurait aucune portance. Grâce à la CFD, nous pouvons analyser, comprendre et prédire les fluides qui composent presque chaque partie de notre monde.
Exemples de la mécanique des fluides numériques
La CFD est utilisée partout où il est nécessaire de prévoir l'écoulement des fluides et le transfert de chaleur, ou de comprendre les effets de l'écoulement des fluides sur un produit ou un système. La CFD analyse différentes propriétés de l'écoulement des fluides, telles que la température, la pression, la vitesse et la densité, et peut être appliquée à divers problèmes d'ingénierie dans tous les secteurs, y compris :
Aérospatiale et Défense : La CFD permet de modéliser le flux d'air autour de l'avion pour prédire la portance et la traînée, ce que l'on appelle l'aérodynamique externe. Cette étude est importante, car les entreprises cherchent à optimiser la conception des avions pour améliorer leurs performances et réduire leur consommation de carburant. La CFD peut également simuler des systèmes complexes à l'intérieur de l'avion, comme la circulation de l'air dans la cabine, pour en analyser sa qualité. Les applications clés incluent le refroidissement avionique, l'aéro-optique, l'aérodynamique externe, le chauffage, la ventilation et la climatisation de la cabine et la propulsion.
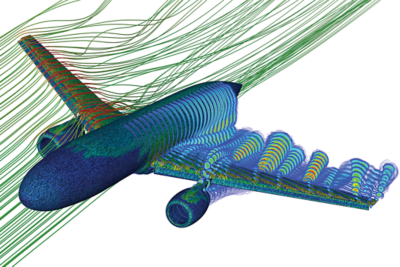
Simulation Ansys Fluent d'une étude aérodynamique externe pour un avion commercial.
Automobile : Dans les véhicules électriques, où les moteurs électriques et l'électrochimie des batteries créent des intersections complexes entre les éléments mécaniques, la chimie et le génie électrique, la CFD nous permet de mener des études thermiques détaillées dans tout le système multiphysique. Cela peut aider les ingénieurs à prévoir l'efficacité du refroidissement du moteur et à réduire l'emballement thermique de la batterie qui peut provoquer des incendies. Les applications clés incluent la lubrification de la boîte de vitesses, les capteurs autonomes, l'aéroacoustique, l'aérodynamique externe, la modélisation de batterie et le refroidissement du moteur électrique.

Modèle de pilote résolu à l'aide du solveur de processeur graphique Ansys Fluent
Nouvelle énergie : Jouant un rôle clé dans la décarbonisation, l'hydrogène représente un carburant précieux pour créer une planète plus propre. La CFD nous permet de modéliser l'ensemble de la chaîne de valeur de l'hydrogène, de la production au stockage, en passant par le transport et la consommation. La CFD peut mener des études exploratoires pour découvrir comment l'hydrogène et d'autres carburants alternatifs peuvent être utilisés dans les moteurs conventionnels et pour déterminer l'efficacité des options de carburants alternatifs. Les applications clés incluent l'électrolyse PEM, la production d'hydrogène, le transport, le stockage et la consommation, et l'utilisation des batteries à combustible.

Étude de combustion réalisée dans Ansys Fluent
Santé : Dans le domaine biomédical, la CFD peut analyser les flux de fluides dans le corps humain, tels que le flux sanguin dans le système circulatoire et le flux d'air dans le système respiratoire. Elle peut également être utilisée pour accélérer le développement de dispositifs médicaux et évaluer l'efficacité potentielle de nouveaux médicaments. Les applications clés incluent le flux cardiovasculaire, le système respiratoire et les produits biopharmaceutiques.
Fonctionnement de la dynamique des fluides numériques
Il existe de nombreuses approches différentes pour résoudre l'écoulement de fluides à l'aide d'un ordinateur. Avant de commencer, vous devez déterminer quelle méthodologie vous utiliserez de manière globale, c'est-à-dire quelles équations principales seront résolues. Ce choix limitera les approches de calcul disponibles. En supposant qu'une approche continue est choisie (ce qui est assez courant), il existe 3 principales étapes.
Tout d'abord, le domaine d'écoulement de fluides (la région continue à calculer) est identifié (généralement représenté par un modèle CAO). Ensuite, un maillage est appliqué pour disséquer le domaine en cellules bien définies. Enfin, la version discrétisée des équations de fluide principales est résolue par l'ordinateur à l'intérieur de chaque cellule. Dans le contexte du calcul haute performance (HPC), une étape facultative consiste à affecter différents groupes de cellules à différents ordinateurs pour un traitement parallèle.
1. Identifier le domaine d'écoulement des fluides à résoudre

2. Discrétiser le domaine selon la taille de maillage et l'espacement de grille souhaités

2. Affecter des processeurs à différentes régions et appliquer les équations de calcul appropriées
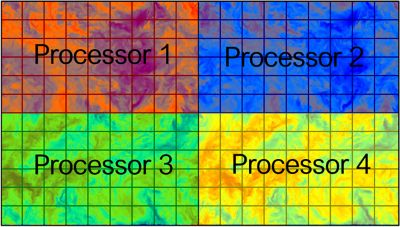
Défis de la modélisation de l'écoulement des fluides
La nature compliquée de l'écoulement des fluides rend sa modélisation sur un ordinateur intrinsèquement difficile. Les interactions multiphysiques, la non-linéarité et l'instabilité sont quelques-unes des complexités qui rendent l'analyse des fluides si difficile.
Interactions multiphysiques : Les fluides ne circulent généralement pas isolément : ils circulent à l'intérieur, à travers et autour de structures. Pensez aux arbres bougeant dans le vent. Quand l'arbre est en mouvement, il change le vent, et le vent change l'arbre. Ce problème couplé de fluide interagissant avec une structure nécessite une approche multiphysique de la modélisation.
Les logiciels Ansys CFD, tels que Fluent et LS-DYNA, peuvent résoudre des problèmes d'interaction fluide-structure comme celui-ci (parfois couplé avec un solveur de mécanique structurelle, comme Ansys Mechanical). Et même en considérant le fluide de façon isolée, de nombreux scénarios réels impliquent de multiples fluides (par exemple, des bulles d'air s'élevant dans l'eau) et/ou des modifications de la composition chimique d'un fluide à la suite de réactions (par exemple, le flux de combustion à l'intérieur d'un moteur d'avion ou les réactions chimiques se produisant dans la batterie de votre voiture). Ansys Fluent est particulièrement bien adapté pour modéliser ces situations.
Non-linéarité : En mécanique des fluides, cette propriété des équations physiques principales signifie que le fluide interagit avec lui-même. La plupart des flux d'intérêt technique sont naturellement turbulents. La turbulence est un exemple de non-linéarité dans la dynamique des fluides, car elle affecte d'autres quantités comme le transfert de chaleur et la quantité de mouvement, qui à leur tour affectent la turbulence. Par turbulence (comme dans les avions), nous entendons que l'écoulement est aléatoire, chaotique et non déterministe.
Ce caractère aléatoire explique pourquoi l'un des éléments clés de la dynamique des fluides numériques est le mot « numérique ». En raison de la non-linéarité et de la turbulence, il n'existe pas de méthode traditionnelle, à l'aide d'un papier et d'un crayon, pour résoudre ces équations. Elles doivent être traitées par ordinateur (sauf pour quelques flux laminaires simples avec une faible dimensionnalité). Cependant, la réponse à un problème de CFD n'est pas une solution, elle résulte simplement du calcul effectué par l'ordinateur après avoir transformé un tas de calculs en formules d'algèbre.
Instabilité : Une caractéristique inhérente à la turbulence est l'instabilité. Cela signifie que les quantités de flux à n'importe quel point fixe de l'espace changent avec le temps. Si cette instabilité est importante (par exemple, votre voiture roule sur l'autoroute), une simulation très précise nécessite une solution résolue en temps réel, ce qui augmente considérablement le coût.
Le phénomène généralisé de turbulence a intrigué les scientifiques et les ingénieurs pendant plusieurs générations. Ce concept complexe a été qualifié par le physicien théorique lauréat du prix Nobel, Richard Feynman, de « problème non résolu le plus important de la physique classique ». Bien que la CFD ne résout pas le problème de la turbulence d'un point de vue mathématique, elle permet aux ingénieurs de créer des modèles qui tiennent compte des effets de la turbulence dans leurs conceptions.
Histoire de la dynamique des fluides numériques
L'étude de la dynamique des fluides numériques a commencé au début du XXe siècle lorsque des modèles mathématiques ont été développés pour la première fois pour traiter l'écoulement des fluides. Avec l'émergence des ordinateurs au milieu du XXe siècle, le domaine a rapidement évolué grâce à leur vitesse de calcul et à leur capacité à modéliser des problèmes de plus en plus complexes.
Premiers développements (années 1900-1940) :
Les équations de base sur l'écoulement des fluides, connues sous le nom d'équations de Navier-Stokes, sont développées. Ces équations fournissent le cadre théorique pour comprendre le comportement des fluides.
Émergence des ordinateurs (années 1950-1960) :
Ce tournant dans la CFD a permis d'effectuer des calculs complexes à grande vitesse et d'obtenir des réponses aux problèmes d'écoulement des fluides autrefois considérés comme impossibles à résoudre.
Méthodes numériques (années 1960-1970) :
L'application de méthodes numériques a permis aux chercheurs de diviser un domaine en une grille d'éléments plus petits pour résoudre les propriétés des fluides dans chaque élément. Cela a permis d'analyser des géométries et des conditions aux limites plus complexes.
Calcul intensif (HPC) (années 2000 à aujourd'hui) :
Avec les avancées du HPC, il est possible d'exécuter des modèles CFD plus grands et plus complexes en moins de temps. L'énorme puissance de traitement du HPC permet aux ingénieurs d'effectuer des calculs de grande ampleur sur des processus complexes, tels que l'analyse d'un avion entier en vol.
Équations principales de CFD
Pour beaucoup de personnes, le mouvement des fluides n'est pas intuitif, car les fluides se déplacent de manière très différente des objets solides. Si vous lancez une balle dans une pièce, elle ne change pas de forme ou de masse. Mais vous ne pouvez pas « jeter » de l'air de la même manière. Les équations principales de CFD nous aident à compenser la forme arbitraire et la nature imprévisible des fluides.
Les équations de Navier-Stokes, nommées d'après Claude-Louis Navier et George Gabriel Stokes, sont des équations aux dérivées partielles décrivant le mouvement des fluides. Développées au milieu du XIXe siècle, ces équations de base permettent de comprendre la mécanique des fluides et sont utilisées pour modéliser tous les types d'écoulements de fluides, tels que l'écoulement d'air autour d'une aile et l'écoulement de carburant dans un moteur. Elles sont considérées comme les principales équations pour la modélisation du comportement des fluides et sont basées sur les équations de conservation de la masse, de la quantité de mouvement et de l'énergie.
1. Conservation de la masse : Équation de continuité
Selon cette équation, la masse d'un volume donné de fluides doit rester constante, sauf s'il y a un flux entrant ou sortant de masse :
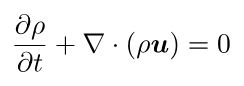
Où ⍴ est la densité du fluide, t est le temps, u le vecteur de vitesse et ∇ l'opérateur gradient.
2. Conservation du mouvement : Deuxième loi de Newton
L'équation du mouvement indique que le taux de changement de mouvement dans un volume de fluide est égal à la somme des forces agissant sur celui-ci, y compris la pression et la gravité. Pour un fluide incompressible à viscosité constante, nous pouvons le traduire comme suit :
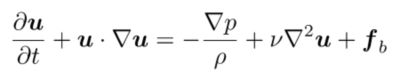
Où p est la pression statique, v est la viscosité et ƒb sont les forces corporelles (typiquement la gravité).
3. Conservation de l'énergie : Première loi de la thermodynamique
Selon l'équation de l'énergie, le changement de l'énergie totale du fluide doit être égal à l'énergie ajoutée ou retirée du système (par exemple, par transfert de chaleur conductif ou convectif).
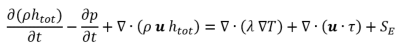
Où htot est l'enthalpie totale, λ la conductivité, T la température et SE les sources externes d'énergie. Le terme ∇ ∙ ( u ∙ t ) est le terme de travail de viscosité et représente le travail dû aux contraintes visqueuses
Avancées en matière de CFD
Le potentiel de la CFD n'est limité que par la puissance du matériel informatique. Comme les avancées matérielles et logicielles permettent la transition des calculs scientifiques des processeurs vers les GPU, y compris l'application de plusieurs GPU pour les simulations CFD, des avancées massives sur la vitesse et la précision sont possibles. Les implémentations multi-GPU entièrement natives accélèrent encore les simulations de CFD, ce qui permet d'atteindre de nouveaux niveaux de performances tout en réduisant les coûts matériels et la consommation d'énergie.










