Que sont les circuits RLC ?

Les circuits RLC sont des circuits électriques dans lesquels des résistances, des inductances et des condensateurs sont connectés en série ou en parallèle. Leur nom provient des symboles utilisés pour représenter ces éléments dans les schémas électriques, à savoir « R » pour les résistances, « L » pour les inductances et « C » pour les condensateurs.

Les systèmes de communication modernes combinent des circuits RLC avec des éléments actifs tels que des transistors et des diodes pour former des circuits intégrés complets. Dans les circuits intégrés, les circuits RLC fonctionnent comme des filtres, des amplificateurs ou des oscillateurs, reposant sur des caractéristiques telles que la résonance et l'amortissement pour fonctionner. Dans les récepteurs radio, par exemple, les circuits RLC effectuent un filtrage passe-bande, ce qui permet à l'utilisateur de régler des fréquences radio spécifiques à l'exclusion des autres.

Les circuits RLC sont également connus sous le nom de circuits de second ordre, en raison du fait que leurs concepteurs utilisent des équations différentielles de second ordre pour caractériser les tensions et les courants qui y circulent. En outre, chaque élément R, L et C de ces circuits peut être disposé dans un certain nombre de topologies différentes, les plus simples étant des topologies série et parallèle.

Dans les circuits RL et RC purs, un seul élément de stockage d'énergie est présent sous la forme d'une inductance (L) ou d'un condensateur (C). Dans ces deux cas, les concepteurs de circuits n'ont besoin de spécifier qu'une seule condition initiale, ce qui donne des équations différentielles de premier ordre.

En revanche, les circuits RLC contiennent les deux éléments de stockage d'énergie, ce qui requiert deux conditions initiales et donne lieu à des équations différentielles de second ordre. Ces conditions initiales concernent les tensions et courants initiaux présents dans le circuit.

Il est également intéressant de noter que, jusqu'au début du XXe siècle, on pensait que les équations différentielles de second ordre fournissaient une description complète des comportements des systèmes physiques. Cependant, grâce aux travaux de Max Planck pour formuler les principes de la mécanique quantique, cette vision a désormais changé.

Néanmoins, les équations différentielles de second ordre continuent de fournir des descriptions précises des comportements de nombreux systèmes physiques. Par exemple, dans le cas d'un pendule en mouvement, l'énergie potentielle dans le champ gravitationnel est convertie en énergie cinétique lorsque le pendule est relâché, avant de se transformer à nouveau en énergie potentielle lorsqu'il atteint sa hauteur maximale. Au fur et à mesure que le pendule dissipe de l'énergie (due à la friction), il s'arrête progressivement.

Il se trouve que les équations différentielles de second ordre fournissent des descriptions précises des systèmes dans lesquels il y a un échange périodique d'énergies, comme illustré dans le système du pendule. Cet échange périodique d'énergie reflète les comportements des circuits RLC, dans lesquels il existe un échange périodique entre les champs d'énergie électrique et magnétique.

Les circuits RLC incorporant des résistances, des inductances et des condensateurs forment la base de la conception des circuits électriques. Chacun de ces éléments présente des caractéristiques physiques spécifiques qui contribuent au comportement global du circuit.

Résistances

Les résistances sont des éléments de circuit localisés qui « résistent » à la circulation des courants, provoquant ainsi une chute de tension. Elles se caractérisent par une résistance constante (mesurée en ohms) indépendante de la fréquence d'un signal appliqué. Les résistances sont indispensables pour maintenir un équilibre dans un circuit RLC.

Inductances

Les inductances sont généralement construites à partir de bobines de fil, stockant l'énergie dans un champ magnétique lorsque le courant passe à travers le fil. Elles s'opposent aux variations de courant, où le degré d'opposition est connu sous le nom de réactance inductive (mesurée en ohms). Cette réactance inductive dépend de la fréquence d'un signal appliqué. Elle augmente à mesure que la fréquence augmente, et vice versa.

Condensateurs

Alors que les inducteurs stockent de l'énergie dans un champ magnétique, les condensateurs la stockent dans un champ électrique. Les condensateurs s'opposent aux variations de tension où le degré d'opposition est connu sous le nom de réactance capacitive (également mesurée en ohms). La réactance capacitive dépend également de la fréquence : elle diminue avec la fréquence croissante, et vice versa.

Les circuits RLC comprennent deux composants principaux, des sources d'alimentation et des résonateurs. De plus, il existe deux types de sources d'alimentation - Thévenin et Norton - et deux types de résonateurs - LC série et LC parallèle. Les circuits RLC série et parallèle présentent chacun des caractéristiques distinctes, ce qui les rend adaptés à des applications spécifiques.

Caractéristiques des circuits RLC série

Dans un circuit RLC en série, des résistances, des inductances et des condensateurs sont disposés sur un seul chemin de circuit, de sorte que le courant circulant à travers chaque composant reste inchangé tandis que les tensions varient. L'effet net est le suivant :

• Aux bornes d'une résistance, la tension est en phase avec le courant.
• À travers une inductance, la tension devance le courant de 90°.
• Aux bornes d'un condensateur, la tension retarde le courant de 90°.

En conséquence, la tension totale aux bornes du circuit n'est pas la somme algébrique des tensions aux bornes de chaque composant, mais plutôt leur somme vectorielle. Ces tensions peuvent être tracées sur un diagramme de phase, en utilisant le vecteur courant pour référence.

La loi de tension de Kirchhoff (KVL) stipule que la somme des tensions dans un circuit fermé est égale à la somme des forces électromotrices (CEM) dans ce circuit. Par conséquent, la tension source VS (en volts) est :

VS = VR + VL + VC

Étant donné que, dans un circuit RLC en série :

VR = IR

VL = LdI/dt

VC = Q/C

Cela devient :

VS = IR + LdI/dt + Q/C

Où I est un courant, L une inductance, Q une charge électrique et C une capacité.

Tout circuit impose naturellement une certaine résistance à la circulation du courant. C'est ce qu'on appelle l'impédance (en ohms). Celle-ci comprend une partie « résistive » (résistance à la circulation de courant continu) et une partie « réactive » (résistance à la circulation de courant alternatif). Dans un circuit RLC en série, elle est exprimée comme suit :

Z = √R2 + (XL2 - XC2)

Où XL est la réactance inductive (opposition au passage du courant alternatif dans l'inducteur) et XC est la réactance capacitive (opposition à la tension alternative au niveau du condensateur).

Les réactances inductives et capacitives dépendent toutes deux de la fréquence, de sorte que : 

• Lorsque XL> XC, la réactance globale dans le circuit devient inductive et la tension devance le courant avec un déphasage de 90°. 
• Lorsque XL< XC, le circuit devient capacitif et la tension retarde le courant de 90°.  
• Lorsque XL = XC, le circuit devient résonant. Ceci a un certain nombre d'applications importantes dans les circuits électroniques.

Caractéristiques des circuits RLC parallèles

Dans un circuit RLC parallèle, la tension reste la même entre les composants R, L et C, tandis que le courant circulant dans chaque composant peut varier. Un circuit RLC parallèle est l'inverse d'un circuit série ; cependant, son traitement mathématique est plus complexe.

Le courant total circulant dans le circuit n'est pas égal à la somme algébrique des courants circulant dans chaque élément, mais plutôt à leur somme vectorielle.

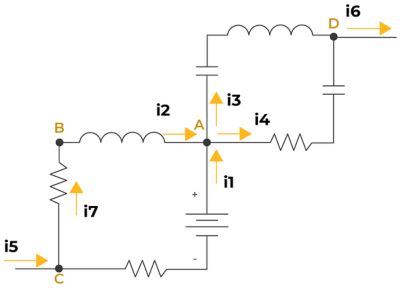
La loi des courants de Kirchhoff (KCL) stipule que la somme des courants circulant à travers un nœud dans un circuit est égale à zéro. Par conséquent, le courant source à du circuit est exprimé par :

IS - IR - IL - IC = 0

Et l'impédance est exprimée par :

1/Z = √(1/R)2 + (1/XL - 1/XC)2

Il convient de noter que l'expression ci-dessus est l'inverse de l'équation de l'impédance dans un circuit RLC en série. En effet, du fait de la relation de dualité qui existe dans les circuits électriques, les propriétés d'un RLC parallèle reflètent celles d'un RLC série. Par conséquent, l'impédance d'un circuit RLC parallèle est le dual de celle d'un circuit RLC en série, et les expressions suivent la même forme générale.

L'inverse de l'impédance (1/Z) est appelé admittance (mesurée en siemens). Elle offre un moyen plus pratique de calculer les impédances dans les circuits parallèles, en particulier lorsque plusieurs branches sont impliquées. L'admittance totale dans les circuits parallèles est simplement la somme des admittances élémentaires. Réciproquement, dans les circuits en série, l'impédance totale est la somme des impédances élémentaires.

À titre d'information, l'inverse de la résistance (1/R) est appelé la conductance, et l'inverse de la réactance (1/X) est appelé la susceptance.

Différences entre les circuits RLC série et parallèle

Comme indiqué précédemment, les formules de circuit pour les configurations série et parallèle sont l'inverse l'une de l'autre. Cela aide les concepteurs de circuits à déterminer si une configuration en série ou en parallèle est plus pratique pour une conception particulière. Les tableaux suivants décrivent les principales différences entre les circuits RLC série et parallèle :

Fondamentalement, il existe deux paramètres qui décrivent le comportement des circuits RLC, à savoir la fréquence de résonance et le facteur d'amortissement. Les ingénieurs peuvent déduire d'autres paramètres, y compris la bande passante et le facteur Q, à partir de ces deux premiers paramètres.

Résonance dans les circuits RLC

Une caractéristique importante des circuits RLC est la capacité de résonner à des fréquences spécifiques, connues sous le nom de fréquences de résonance. Les systèmes physiques présentent des fréquences naturelles auxquelles ils vibrent plus facilement. À la résonance (en présence ou en l'absence d'une source d'excitation), les vibrations sont fortement amplifiées, ce qui entraîne des transferts d'énergie efficaces.

Dans un circuit RLC, l'énergie stockée dans le champ électrique d'un condensateur peut être transférée et stockée dans le champ magnétique entourant une inductance, et vice versa. Ce transfert peut se produire périodiquement, entraînant un circuit RLC oscillant. À la résonance, la fréquence angulaire Ω (en radians) est exprimée par :

ω = 1/√LC

À la résonance, la réactance inductive est égale à la réactance capacitive, et l'impédance totale du circuit (qui est un nombre complexe) devient nulle.

Par conséquent, dans un circuit RLC en série, l'impédance est minimale, alors que dans un circuit parallèle, elle est maximale. 

Il est essentiel de comprendre et d'appliquer la résonance dans les circuits RLC pour concevoir des systèmes électroniques efficaces et performants, en particulier dans les domaines des communications, des systèmes d'alimentation et du traitement du signal. Les principales applications de la résonance sont les suivantes :

• Sélection de fréquence : À la résonance, les circuits RLC peuvent répondre à des signaux de fréquences spécifiques à l'exclusion d'autres fréquences, par exemple, le syntoniseur d'une radio.
• Filtrage : Les circuits RLC peuvent fonctionner comme différents types de filtres, filtres passe-bande, coupe-bande, passe-bas ou passe-haut. Ces circuits peuvent également servir de filtres anti-bruit dans les circuits intégrés. Ils peuvent également fonctionner comme des circuits réjecteurs, supprimant les courants à des fréquences spécifiques, et ce type de circuit parallèle est connu sous le nom d'antirésonateur.
• Multiplication de la tension : Si la résistance est minimale, les tensions aux bornes de l'inducteur et du condensateur peuvent être plusieurs fois supérieures à la tension d'entrée. Cet effet multiplicateur de tension est proportionnel au facteur Q du circuit.
• Adaptation d'impédance : À la résonance, l'impédance d'un circuit RLC en série est purement résistive et atteint son minimum, alors que dans un circuit RLC en parallèle, elle atteint son maximum. Ceci peut être utilisé pour l'adaptation d'impédance.
• Transfert de puissance : Comme les circuits RLC en série atteignent un transfert de puissance maximal à la résonance, ils sont essentiels pour les applications nécessitant un transfert d'énergie efficace.
• Circuits d'oscillateur : Les circuits RLC sont couramment utilisés dans les applications d'oscillateur, où des oscillations soutenues à une fréquence spécifique sont requises. Dans ces cas, la résistance du circuit est minimisée (pour les circuits en série) ou maximisée (pour les circuits en parallèle) pour réduire l'amortissement et obtenir un circuit LC idéal.

Amortissement dans les circuits RLC

L'amortissement fait référence à la diminution des amplitudes des oscillations dans les systèmes RLC au fil du temps (en raison des résistances). Par conséquent, les résistances jouent un rôle essentiel dans la dissipation de l'énergie dans les circuits RLC. Elles influencent également la capacité du circuit à résonner naturellement (en l'absence de source d'excitation).

Ainsi, les ingénieurs observent trois types de réponses d'amortissement dans les circuits RLC :

• Circuits sous-amortis, caractérisés par une décroissance lente des oscillations
• Circuits suramortis, où les oscillations cessent rapidement
• Circuits à amortissement critique, où les oscillations cessent juste avant le temps critique nécessaire pour atteindre les oscillations en régime permanent
• Pour les circuits à amortissement critique, \zeta = 1

Le coefficient d'amortissement sans dimension est un paramètre clé qui permet aux ingénieurs de caractériser l'amortissement dans les circuits RLC. Dans les circuits oscillateurs, les ingénieurs cherchent à réduire l'amortissement en minimisant la résistance dans un circuit en série tout en maximisant la résistance dans un circuit parallèle. Dans les filtres passe-bande, le coefficient d'amortissement est réglé pour correspondre à la largeur de bande souhaitée : une valeur plus élevée entraîne une bande passante plus large et vice versa.

Les paramètres dérivés dans les circuits RLC comprennent la largeur de bande et le facteur Q.

Bande passante

La largeur de bande décrit la plage de fréquences à laquelle résonne un circuit RLC. Il s'agit d'un paramètre clé dans la conception des filtres, où un changement rapide d'impédance près de la résonance peut être utilisé pour laisser passer ou bloquer les signaux proches de la fréquence de résonance ; un effet visible dans les filtres passe-bande et coupe-bande, respectivement.

La bande passante représente l'écart de fréquence entre les fréquences de coupure, généralement définies comme les fréquences auxquelles la puissance traversant le circuit est moitié moins élevée que la puissance à la résonance. 

Les ingénieurs ajustent l'amortissement dans les circuits de filtrage pour correspondre à la bande passante souhaitée. Un amortissement élevé permet d'obtenir un filtre à large bande. À l'inverse, un faible amortissement conduit à un filtre à bande étroite.

Facteur Q

Le facteur Q sans dimension décrit le taux d'amortissement d'un système oscillant. Il est défini comme le rapport entre l'énergie initiale stockée dans le système et l'énergie dissipée en un radian d'un cycle d'oscillation.

Un facteur Q plus élevé représente une perte d'énergie plus faible, les oscillations s'estompant plus lentement (bande étroite, sous-amortie), tandis qu'un facteur Q plus faible représente un réseau dissipatif (bande large, suramortie). Parmi les exemples de systèmes à facteur Q élevé, on trouve les horloges, les lasers et les diapasons, ces derniers ayant un facteur Q de l'ordre de 1000. Certains lasers à facteur Q élevé atteignent des valeurs de 1011 ou plus.

Les circuits RLC qui intègrent des résistances, des inductances et des condensateurs forment la base de la conception des circuits. En tirant parti des caractéristiques de résonance et d'amortissement des circuits, les ingénieurs peuvent concevoir une variété de circuits pour une utilisation dans une gamme d'applications. Par conséquent, la compréhension et la caractérisation des circuits RLC sont essentielles pour la conception, l'analyse et l'optimisation de circuits assimilés à une variété de systèmes électroniques et de communications.

Dans les circuits RLC, le couplage électromagnétique est un facteur critique qui a un impact sur les performances de ces circuits, affectant la réponse en fréquence, le transfert de puissance, l'amortissement et d'autres caractéristiques.

C'est pourquoi, en matière de conception de circuits, le logiciel Ansys Exalto ® est une solution logicielle d'extraction RLCk post-LVS qui permet aux concepteurs de capturer avec précision la diaphonie entre les différents blocs de la hiérarchie de conception en extrayant les parasites à éléments localisés et en générant un modèle précis de couplage électrique, magnétique et de substrat. Le logiciel Exalto s'interface avec la plupart des logiciels LVS et peut compléter l'outil d'extraction RC de votre choix.

En outre, le logiciel Ansys RaptorH ™ est un logiciel de modélisation électromagnétique pré-LVS permettant la modélisation électromagnétique haute capacité de SOC RF et numériques haute vitesse, y compris les réseaux électriques, les blocs entièrement personnalisés, les inductances en spirale et les arbres d'horloge. Il intègre le moteur de simulation électromagnétique de pointe Ansys HFSS™ avec le moteur Ansys RaptorX, spécifiquement optimisé pour le silicium.

Ressources connexes